Die zwei Elektronenringe Teil 1
Um den Kurvenverlauf der ersten Ionisierungsenergie I1 zu verstehen, muss die Verteilung der Elektronen um den Atomkern herum bekannt sein. Im bislang geltenden Standardmodell geht man von einer verschwommenen Elektronenwolke aus, wobei das Einzelelektron sich in Orbitalen oder sogar Hybridorbitalen aufhält. Außerdem gibt es in diesen Orbitalen für die Elektronen keine festen Plätze, sondern nur sogenannte Aufenthaltswahrscheinlichkeiten.
In meinem neuen Modell befinden sich die Elektronen auf zwei Elektronenringen, einem inneren kleineren und einem äußeren größeren. Jeder Ring besitzt insgesamt 16 verschiedene Sektoren. Es handelt sich um zwei rote, sieben blaue und sieben gelbe Sektoren (siehe Abb.1). Jeder rote Sektor eines Rings ist in der Mitte nochmals unterteilt, so dass pro Ring vier rote Bezirke entstehen. Jeder blaue/gelbe Sektor ist ebenfalls in der Mitte unterteilt in zwei Bezirke, a und b.
Für die Anordnung der beiden Elektronenringe zueinander gibt es mehrere Möglichkeiten. Diese harren der weiteren Erforschung. Abb. 6 zeigt die Möglichkeit, die ich derzeit favorisiere:
Die beiden Elektronenringe sind in einer Ebene gegeneinander um 90 Grad gedreht. Außerdem können sie zwischen 0° und 90° zueinander gewinkelt sein, so dass im Fall einer chemischen Bindung alle Bindungswinkel möglich sind und auch jeder Elektronenplatz dafür zugänglich ist. Befänden sich die beiden Ringe ausschließlich in einer einzigen Ebene, wären für die beiden Bindungspartner ihre inneren Elektronenringe durch die äußeren blockiert.
In den roten Sektoren befinden sich die Elemente aus den Zweiergruppen des neu eingeteilten Periodensystems, in rot 1 und 3 die ungeradzahligen, in rot 2 und 4 die geradzahligen. In den blauen und gelben Sektoren befinden sich die Elemente aus den Achtergruppen, in den blauen die ungeradzahligen, in den gelben die geradzahligen.
Ein Einzelelektron besteht aus insgesamt 28 gleichen Teilen. Die chemischen Elemente der roten Bezirke bestehen aus 4 x 7 Achtundzwanzigstelelektronen (7/28 x 4 = 28/28 = 1 Elektron). Beispiel Wasserstoff: Das H-Atom ist ungeradzahlig, belegt also auf den beiden Ringen die Bezirke rot 1 und rot 3, die Bezirke rot 2 und rot 4 bleiben frei. Da jeder belegte Bezirk ¼ e– an Ladung trägt und jeder Ring zwei rote Bezirke für ungeradzahlige Elemente besitzt, hat das H-Atom seine Ladung je hälftig auf jeden Ring verteilt.
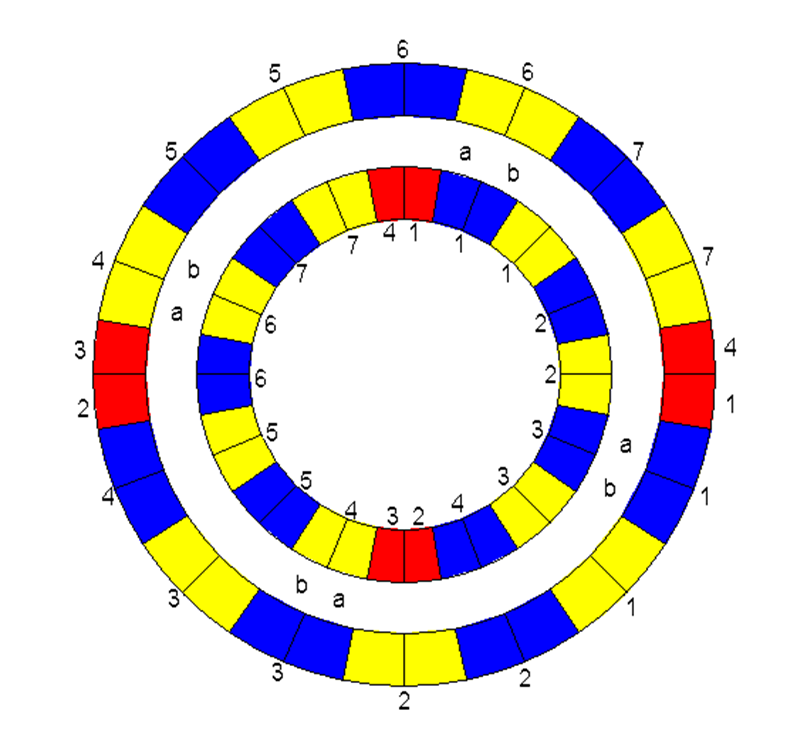
Abb.6:Die beiden Elektronenringe: Die Achtundzwanzigstelelektronen sitzen in den roten, gelben und blauen Sektoren. Die roten Sektoren sind zwischen innen und außen um 90° versetzt. Das hat Auswirkungen auf das Prinzip der Elektrostatik und auf die elektrische Leitfähigkeit der Elemente.
Beispiel Helium: Das He-Atom ist geradzahlig, belegt also zusätzlich zum H-Atom die vorher freien Bezirke rot 2 und rot 4. Analog zum H-Atom hat auch das He-Atom seine Ladung je zur Hälfte auf die Ringe verteilt. Insgesamt trägt jetzt jeder innere und jeder äußere rote Bezirk 7 Achtunzwanzigstelelektronen oder je ¼ e– an Ladung. Beide Ringe tragen an Ladung 1 e–, wobei die eine Hälfte aus der anfänglichen Wasserstoffkonfiguration stammt, die andere Hälfte aus der hinzukommenden Heliumkonfiguration.
Jeder rote Bezirk bietet Platz für 7 ¼ – Elektronen. Nachdem Wasserstoff und Helium ihre beiden Elementarladungen je hälftig auf beide Ringe verteilt haben, gibt es in jedem roten Bezirk (innen und außen) noch sechs freie Plätze für ¼ – Elektronen.
Die restlichen roten Elemente (Kalium, Calcium, Rubidium, Strontium, Caesium, Barium, Francium und Radium und die Lücken nach 71 und vor 72 sowie die Lücken nach 103 und vor 104) verteilen ihre Elementarladungen nur noch auf einem Elektronenring (Kalium, Calcium, Rubidium, Strontium, Caesium, Barium außen; Francium, Radium und beide Lücken innen), indem sie in jedem ihrer roten Bezirke zwei Plätze für ¼ – Elektronen einnehmen.
Die Elemente Wasserstoff und Helium unterscheiden sich in ihrer ersten Ionisierungsenergie deutlich von den restlichen Elementen in den roten Bezirken. Um das Elektron des Wasserstoffs herauszulösen bedaf es 13,6 eV (allerdings nur theoretischer Wert), für das Elektron von Helium braucht man schon gigantische 24,6 eV (Messwert). Für die restlichen roten Elemente braucht es dagegen nur zwischen 3,9 eV und 6,1 eV. Das spricht dafür, dass es bei Wasserstoff und Helium bedeutend mehr Energie bedarf, ihre Elektronen herauszulösen, da sie diese auf beide Ringe verteilt haben. Befinden sich die ¼ – Elektronen dagegen nur auf einem Elektronenring, muss man viel geringere Energien dafür einsetzen.
Bei den ersten beiden Elementen des Periodensystems – Wasserstoff und Helium – gibt es eine weitere Besonderheit. Beide Elemente kommen in einer Ortho – und einer Paraform vor, die jeweils geringe physikalische Unterschiede aufweisen. Bei allen anderen Elementen im Periodensystem gibt es das nicht. Wasserstoff und Helium haben ihre Elektronenachtundzwanzigstel je hälftig auf beide Ringe verteilt. Alle anderen Plätze auf beiden Ringen sind noch leer. Wasserstoff belegt normalerweise die Bezirke rot 1 und rot 3 auf beiden Ringen. Wenn Wasserstoff aber einmal die Bezirke rot 2 und rot 4 auf beiden Ringen belegt, könnte das die Erklärung für seine Ortho – und seine Paraform sein. Dasselbe gilt für Helium. Da die Zweiergruppenelemente ihre Ladung in der Folge auf nur einen Ring – entweder innen oder außen – verteilen, ist dann kein solcher Wechsel mehr möglich.
In den je sieben blauen und gelben Sektoren eines Elektronenrings befinden sich pro Sektor und chemischem Element vier Achtundzwanzigstelelektronen (4/28 x 7 = 28/28 = 1 Elektron), je zwei in Bezirk a und zwei in Bezirk b. Die Achtundzwanzigstelelektronen eines Elements der blauen/gelben Sektoren befinden sich ausschließlich auf einem einzigen Ring, entweder alle innen oder alle außen.
Als Ladung ausgedrückt trägt jeder blaue/gelbe Sektor für jedes Element 4/28 e– = 1/7 e–. Dieser Wert (allerdings als Masse) wird bei der Berechnung der Elementarteilchen auftauchen.
Daraus ergibt sich nun eine Art Grundwährung: das Elektronenachtundzwanzigstel.
Die Trennung in ungerade (blaue) und gerade (gelbe) Sektoren spiegelt sich im Kurvenverlauf der Achtergruppen von I1 (erste Ionisierungsenergie) wider. Von Element Lithium (3) über Bor (5) zu Stickstoff (7) und Fluor (9) steigt I1 stetig an, genau wie von Element Beryllium (4) über Kohlenstoff (6) zu Sauerstoff (8) und Neon (10).
Dagegen ist I1 bei Element Bor (5) geringer als bei Beryllium (4).
I1 zeigt bei allen nach rechts geschriebenen Achtergruppen stets den gleichen sprunghaften ansteigenden Kurvenverlauf. Dagegen zeigen alle nach links geschriebenen Achtergruppen ganz flache Kurven, weil sich die Elektronenachtundzwanzigstel beider Gruppen auf verschiedenen Ringen befinden. Die Gruppe mit den flachen Verläufen hat ihre Elektronenachtundzwanzigstel auf dem leichter zugänglichen größeren äußeren Ring, die mit den sprunghaften Verläufen auf dem inneren kleineren Ring.
Der Platz pro Achtundzwanzigstelelektron beträgt 0,1°, so dass ein Elektronenring in insgesamt 3600 Abschnitte zu 0,1° unterteilt wird. Die Zahl 3600 weist auf die alte sumerische Maßeinheit des „Sar“ hin und ich vermute, dass in den Elektronenringen ihr eigentlicher Ursprung liegt.
Wie sieht nun die Feinstruktur der roten, blauen und gelben Sektoren aus ?
Jeder rote, blaue und gelbe Sektor ist in der Mitte durch zwei freie Plätze (= Trennwände) zu je 0,1° unterteilt, ebenso die einzelnen Sektoren an ihren Rändern (siehe Kasten 1). Dort, wo die roten an die blauen/gelben Sektoren angrenzen, sind es nicht zwei sondern vier freie Plätze zu 0,1°. Diese Trennwände im Bereich der Atomhülle entsprechen den starken Kernkräften im Bereich des Atomkerns (Gitterlinien als Verbindung der Protonenplätze).
Jeder der vier roten Bezirke eines Elektronenrings besteht aus 98 Abschnitten zu je 0,1°, insgesamt aus 392 Abschnitten. Jeder blaue und gelbe Sektor besteht aus je 224 Abschnitten zu je 0,1°, insgesamt 3136 Abschnitten. Zusammen mit den freien Plätzen in der Mitte und an den Rändern der Sektoren/Bezirke (72) ergibt dies 3600 Abschnitte zu 0,1°.
Von den 3600 Abschnitten können die zur Trennung dienenden freien Plätze (72) nicht mit Elektronenachtundzwanzigsteln belegt werden.
Vom Rest (3528) wird nur jeder zweite Platz belegt, jeder zweite bleibt frei. Dadurch wird einerseits eine möglichst gleichmäßige Elektronenverteilung bewirkt, andererseits ist garantiert, dass jedes bindende Elektronenachtundzwanzigstel eines Elements/Moleküls für seinen Bindungspartner im Fall einer kovalenten Bindung immer direkt neben sich einen freien Platz zur Verfügung stellen kann.
Kasten 1 zeigt die Feinstruktur eines Elektronenrings, Kasten 2 das Belegungsschema beider Ringe. Der zweite äußere Elektronenring ist in den roten Sektoren voll mit chemischen Elementen belegt, der innere kleinere Elektronenring weist insgesamt 56 Lücken auf.
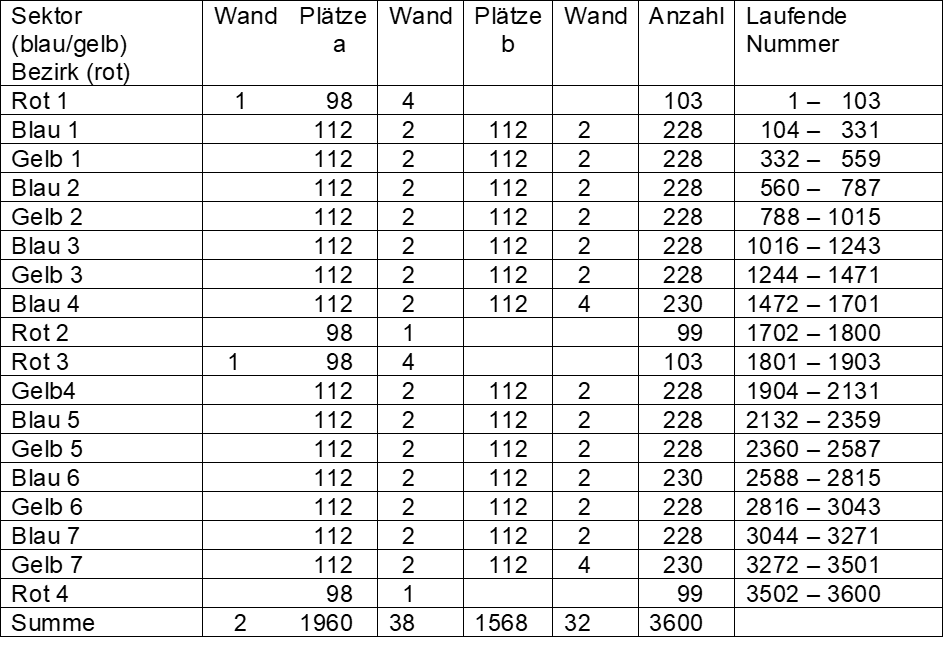
Kasten 1: Feinstruktur eines Elektronenrings
Weiterhin erkennt man (siehe Kasten 2), dass auf beiden Ringen in den blauen Sektoren vier Plätze nicht belegt sind. Innen entspricht das dem freien Elementplatz vor Element 104 (Achtergruppe nach rechts geschrieben), außen dem freien Elementplatz vor Element 72 (Achtergruppe nach links geschrieben).
Die entsprechenden nicht belegten Plätze treten in den gelben Sektoren nur auf dem äußeren Ring auf, da beide korrespondierende Achtergruppen nach links geschrieben sind (freie Elementplätze nach den Elementen 71 und 103).
Die Gesamtkapazität des Systems beider Ringe bietet Platz für 126 Elektronen (insgesamt 7056 Plätze, 3528 x 1/28 e– + 3528 freie Plätze), wobei jeder zweite Platz frei bleibt. 144 Plätze dienen als Wände bzw. Begrenzungen.
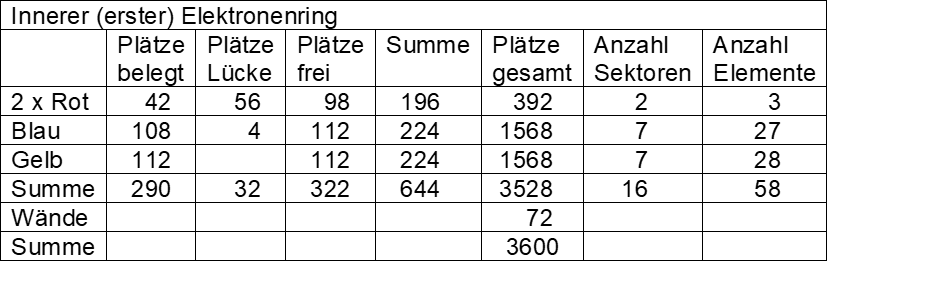
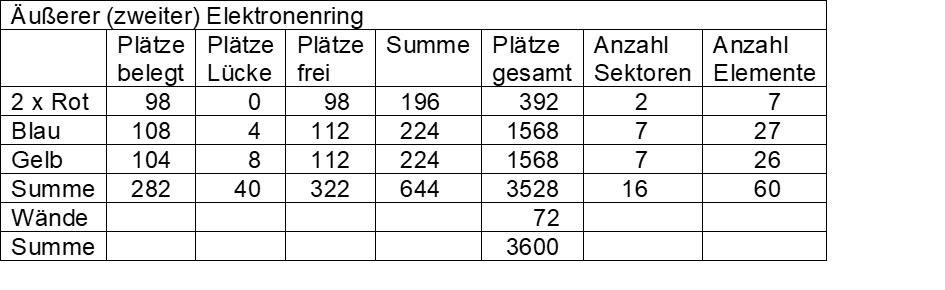
Kasten 2: Belegungsschema der beiden Elektronenringe
Die Zahl 126 korrespondiert mit der Zahl 126 aus dem Neutronenbereich. Hier ist die Grenze zur immer währenden Radioaktivität, die ab dem 127sten Neutron beginnt.
Einerseits garantieren die freien Plätze der Elektronenringe die Bindungsmöglichkeit eines Achtundzwanzigstelelektrons im Molekül bei einer kovalenten Bindung. Andererseits besteht auch die Möglichkeit, dass das gesamte Elektronensystem sich um 0,1° verschiebt. Es sind also zwei um 0,1° unterschiedliche Einstellungen möglich, ohne mit den Begrenzungswänden in Konflikt zu geraten. Es handelt sich um die aus der Radiaesthesie bekannten beiden Polarisationsmöglichkeiten (Rechts- oder Linksdrehung, z.B. bei Wasseradern oder geologischen Verwerfungszonen). Die beiden Einstellungsmöglichkeiten könnten auch eine alternative Erklärung für das Ergebnis des Stern-Gerlach-Versuches bieten, wo Silberatome beim Durchgang durch ein inhomogenes Magnetfeld auf einem Schirm zwei unterschiedliche Flecken hinterlassen. Die eine Hälfte wird zum Nordpol abgelenkt, die andere zum Südpol. Im hier vorliegenden Modell bewirkt der Nordpol für die Silberatome die eine Einstellungsmöglichkeit der Elektronenpartikel, der Südpol die andere und deshalb erfolgt die beschriebene hälftige Aufteilung.
