Die Ruhemassen der Elementarteilchen
Eine auf Herodot zurückgehende Überlieferung besagt, das Quadrat über der Höhe der Cheopspyramide sei flächengleich mit zwei ihrer Oberflächendreiecke (OFD). Im pi-phi-System stimmt das mit h2 = 2 x OFD = 78 400 KE2 (KE = Königliche Elle, 52,3606798 cm) ganz genau.
Im pi-antik-System ergibt sich eine kleine Abweichung, das Verhältnis h2 zu 2 x OFD beträgt nicht genau 1,0 sondern 1,001304167. Dies ist bis auf vier Stellen hinter dem Komma das Verhältnis der Ruhemassen von Neutron und Proton, den Bestandteilen der Atomkerne.
Allein schon das Auftauchen von Daten aus der Atomphysik in der Cheopspyramide, einem Bauwerk aus der fernen Vergangenheit der Menschheitsgeschichte, legt es nahe, diesen Themenbereich näher zu untersuchen.
Da ich dies bereits vor über zwanzig Jahren getan habe, habe ich auch die damals zugänglichen wissenschaftlichen Werte benutzt. Nach Ulshöfer/Hornschuh: „Mathematische Formeln und physikalische Größen“ aus dem Jahr 1995 beträgt das Verhältnis der Ruhemassen von Neutron und Proton 1,001378532.
Ein paar Jahre später (2006) habe ich die damals geltenden Werte der Particle Data Group CODATA 2006/NIST verwendet. Das damalige Verhältnis der Ruhemassen von Neutron und Proton beträgt 1,001378419.
Die neuesten Werte stammen von der Particle Data Group CODATA 2022/NIST. Danach beträgt das Verhältnis 1,00137841946(40). Der Unterschied zwischen den Zahlen von 1995, 2006 und 2022 ist zwar gering und tritt erst ab der siebten Nachkommastelle auf. Gleichwohl hat er mich gezwungen, meine Berechnungen zu überprüfen, mit den neueren Daten zu wiederholen und die Ergebnisse kritisch zu interpretieren.
Die Ruhemassen der Elementarteilchen werden angegeben in Kilogramm, der Maßeinheit der Masse im Meter-Kilogramm-Sekunde-System, oder aber in MeV (Megaelektronenvolt), der Energie, die dieser Masse entspricht.
Nach Ulshöfer/Hornschuh 1995 Kasten 1

Nach CODATA 2006/NIST Kasten 2a

Nach CODATA 2022/NIST Kasten 2b

Die Zahlen in den Klammern hinter den Massewerten geben die Unsicherheit an. Es handelt sich um die Standardabweichung, ausgedrückt in Einheiten der beiden letzten Ziffern des angegebenen Werts. Somit bedeutet 1,6749543(86) x 10-27 kg = 1,6749543 +/- 0,0000086 x 10-27 kg. Damit wird ein Grenzbereich festgelegt, innerhalb dessen ein Wert auf Grund der Messungenauigkeit schwanken kann.
Bei den Daten aus 2006 und 2022 sind mehr Nachkommastellen hinzugekommen und sie unterscheiden sich von den 1995er Daten in der Einheit kg ab der vierten (Elektron) bzw. fünften (Proton, Neutron) Nachkommastelle, in der Einheit MeV ab der zweiten (Neutron) bzw. dritten (Proton, Elektron) Nachkommastelle.
Im Vergleich der 2006er mit den 2022er Werten treten Unterschiede ab der siebten Nachkommastelle auf (Neutron, Proton) und ab der sechsten Nachkommastelle (Elektron), jeweils in der Einheit kg.
Dividiert man den Massewert eines Neutrons in der Einheit Kilogramm durch den eines Protons, so erhält man die oben angegebenen Zahlen 1,001378532 (Jahr 1995), 1,001378419 (Jahr 2006) und 1,001 378 419 46(40) (Jahr 2022).
In der Einheit MeV ergibt sich 1,001378587 (Jahr 1995), 1,00137842 (Jahr 2006) und 1,001378419 (Jahr 2022).
Beim Vergleich der Werte, die aus den Einheiten kg und MeV gewonnen wurden, tritt bei den Angaben aus 1995 ab der achten Stelle hinter dem Komma eine kleine Abweichung auf (kg: letzte drei Ziffern 532 versus MeV: letzte drei Ziffern 587), die es bei den Werten aus dem Jahr 2006 (kg: 9 Nachkommastellen, letzte drei Zahlen 419; MeV: 8 Nachkommastellen, letzte 2 Zahlen 42) und 2022 nicht mehr gibt.
Grenzwerte der Ruhemassen der Elementarteilchen

Berechnet nach Ulshöfer/Hornschuh 1995 Kasten 3
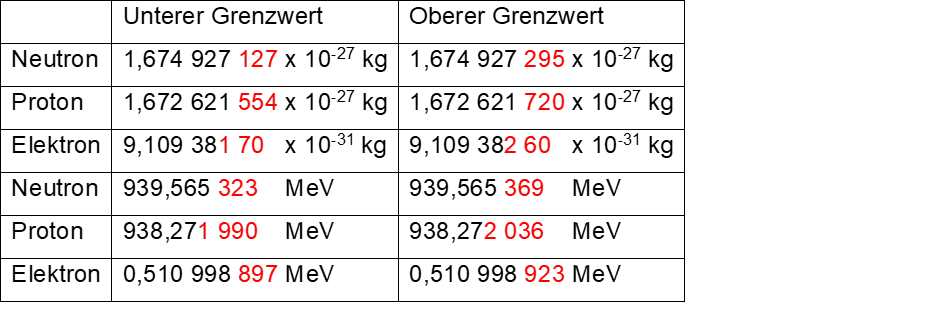
Berechnet nach CODATA 2006/NIST Kasten 4a
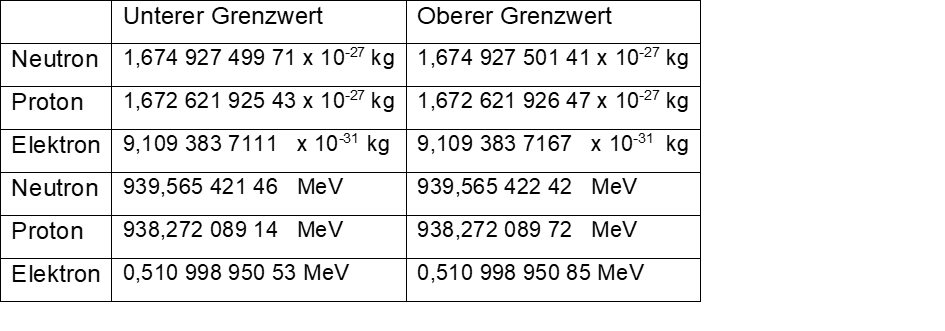
Berechnet nach CODATA 2022/NIST Kasten 4b
Bezieht man jetzt noch die Grenzbereiche ein (Kasten 3, Kasten 4a, Kasten 4b), dividiert also den größten Wert für das Neutron durch den kleinsten Wert für das Proton und den kleinsten Wert für das Neutron durch den größten Wert für das Proton, erhält man die Zahlen aus Kasten 5. Das ist der Grenzbereich, indem das Verhältnis der Ruhemassen von Neutron und Proton als Ausdruck der Messungenauigkeit schwanken kann.
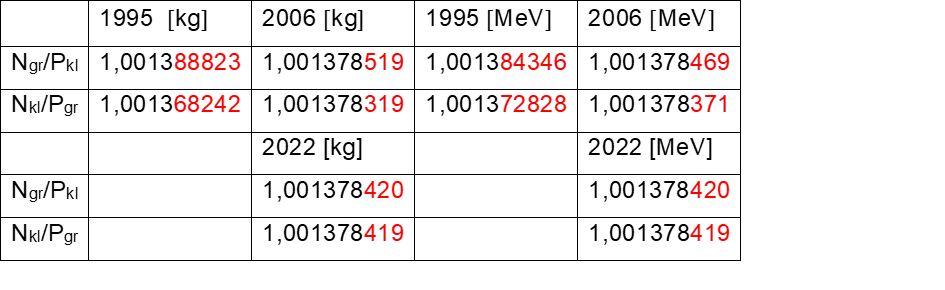
Grenzwerte des Neutron/Proton Masseverhältnis Kasten 5
Wie zu sehen ist, treten bei den 1995er Werten die Unterschiede ab der fünften und bei den 2006er und den 2022er Werten erst bei der siebten Nachkommastelle auf, die Messwerte scheinen um den Faktor 100 besser geworden zu sein. Bei den 2022er Werten gibt es fast gar keine Unterschiede mehr.

Kasten 6
Bei der Wiederentdeckung der geometrischen Verhältnisse der Cheopspyramide war eine Einheit aufgetaucht, die Grundeinheit (1 GE = 1,370820394 m), die einen weiteren Wegweiser in die Atomphysik enthielt, die Sommerfeldsche Feinstrukturkonstante ( 1/137,03599976 ).
Fasst man nun den MeV-Wert des Neutrons als Fläche auf (Energien verhalten sich wie Flächen) und wandelt die Mittelwerte 939,5731 (Jahr 1995, siehe Kasten 1), 939,565346 (Jahr 2006, siehe Kasten 2a) und 939,56542194 (Jahr 2022, siehe Kasten 2b) über die Umrechnungsfaktoren 25/φ4 und 1/φ4 um – man gelangt auf diese Weise vom m2-Bereich über die Einheit KE2 in die Einheit GE2 (siehe Kasten 6) –, so erhält man 499,999374 (Jahr 1995), 499,9952473 (Jahr 2006) und 499,995288 (Jahr 2022). Das erweckte in mir bei der ersten Recherche mit den 1995er Zahlenwerten den Verdacht, es könnte sich hier um die Zahl 500, also um eine glatte Zahl, handeln. Rechnet man die Zahl 500 zurück in die Einheit MeV über φ8/25, erhält man 939,574 276 4. Der obere Grenzwert für das Neutron liegt bei 939,5758 (Jahr 1995, siehe Kasten 3), 939,565 369 (Jahr 2006, siehe Kasten 4a) und 939,565 422 42 (Jahr 2022, siehe Kasten 4b).
Somit liegt der zurück gerechnete Wert 939,5743 (gerundet) innerhalb des zulässigen Grenzbereichs, leider aber nur mit den Zahlenwerten des Jahres 1995. In der CODATA 2006/NIST-Version liegt der obere Grenzwert für das Neutron niedriger. Deshalb ist hier der zurück gerechnete Wert um 9/1000 zu groß. Für die Werte des Jahres 2022 gilt das fast in gleicher Weise.
Woran kann das liegen? Sind die neueren Messdaten zutreffender, die älteren ungenauer und damit falsch und kommt deshalb das Gebiet der Atomphysik in der Cheopspyramide gar nicht vor? Oder unterliegen die Massen der Elementarteilchen mit der Zeit gewissen Veränderungen?
Die geometrischen Verhältnisse in der Cheopspyramide waren immer zu einhundert Prozent exakt. Hier gab es keinerlei Toleranzen, obwohl mit Irrationalzahlen wie φ, φ2 und 6/5φ2 (pi-antik) gerechnet werden musste.
Bei Werten wie dem Erdumfang, dem Polradius und der Anzahl der Tage eines Sonnenjahres wie auch bei der Sommerfeldschen Feinstrukturkonstante aber ergaben sich nicht die exakten heute gültigen Zahlen sondern ausschließlich Näherungswerte. Diese allerdings kamen den heutigen sehr, sehr nahe (siehe Kasten 7).
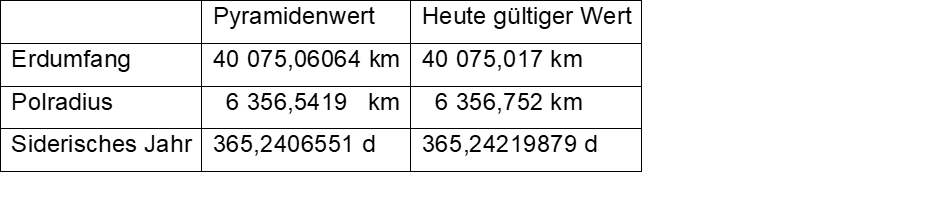
Kasten 7
Wenn die Erbauer der Cheopspyramide in der Lage waren, alle geometrischen Beziehungen ohne jegliche Toleranzen in Stein zu hauen, hätten sie sicherlich auch die ganz genauen Werte für physikalische Konstanten wie die Ruhemassen der Elementarteilchen darstellen können. Wenn wir heute dagegen leicht abweichende Werte vorfinden, könnten diese möglicherweise zur Zeit der Erbauung der Cheopspyramide die exakten Werte gewesen sein. Sollte diese Schlussfolgerung richtig sein, wären damals Feinstrukturkonstante, Polradius und siderisches Jahr um eine Kleinigkeit geringer gewesen als heute, der Erdumfang etwas größer .
Wir hätten damit aber auch eine Art Kalender zur Hand, der uns die genaue Erbauungszeit der Cheopspyramide verraten könnte. Leider kann ich nicht sagen, ob sich die planetare Umlaufzeit der Erde überhaupt ändert und wenn doch, wie lange es braucht, bis sie 16/10000 Tage länger geworden ist. Vielleicht wird die Zukunft ja eine Lösung dieses Problemkomplexes bringen.
Ich will nun mit der weiteren vergleichenden Berechnung der 1995er, 2006er und 2022er Werte fortfahren. Ausgangspunkt ist der vermutete Wert für das Neutron:
500 x φ8/ 25 MeV = 20 x φ8 MeV = 939,574 276 4 MeV
Um jetzt die entsprechenden Werte für das Proton und das Elektron zu finden, steht man vor einigen Schwierigkeiten. Wegen der genannten Grenzbereiche gibt es keine ganz exakten Umrechnungsfaktoren. Ein Beispiel soll das verdeutlichen: Legt man das Neutron auf den Wert 500 fest, so könnte der Wert für das Proton unter Zugrundelegung der 1995er Zahlen zwischen 499,3087839 (= 500 : 1,001384346) und 499,314527 (= 500 : 1,001372828 ) liegen. Aber wo?
Hier hilft wirklich nur probieren. Nachfolgend mein Weg:
Mir war aufgefallen, dass mit den 1995er Zahlen das Proton 1836,15 me (me = Elektronenmasse) betrug. 0,15 liegt dicht beim Wert für 1/7 (0,142857..). Also habe ich das Proton auf den Wert 1836 1/7 me gesetzt. Das sind 12 853/7.
Die Division des Wertes für das Neutron 500 : 1,00130416709 (diese Zahl stammt von der Pyramide und entspricht h2 : 2 x OFD = Pyramidenfaktor) ergibt 499,348765818. Das ist für die Ruhemasse des Protons noch zu groß. Als nächstes wird 499,348765818 durch 12854 dividiert. Das Ergebnis ist 0,03884773345 und diese Zahl wird von 499,348765818 subtrahiert. Das Ergebnis ist 499,309918085, die gesuchte Ruhemasse des Protons. Die Division dieser Zahl durch 12853 ergibt wiederum 0,03884773345 (siehe Kasten 8). Multipliziert man das mit sieben, ergibt sich 0,27193413415, die Ruhemasse des Elektrons in MeV x φ8/25. Kasten 9 gibt die von mir ermittelten Massenwerte für das Neutron, das Proton und das Elektron wieder.
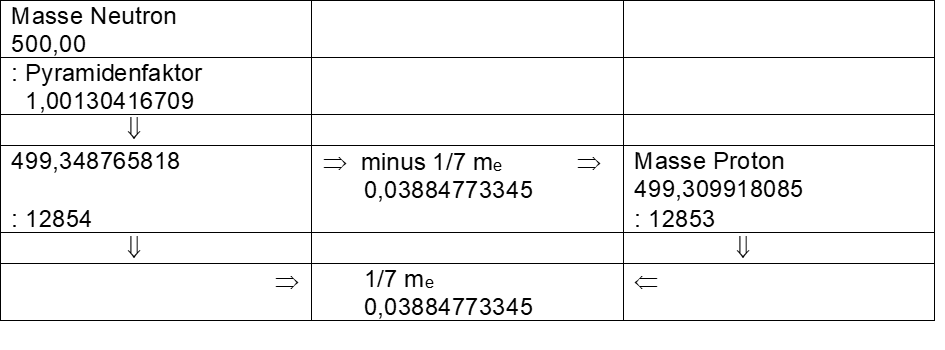
Kasten 8: Weg Neutronenmasse zur Protonenmasse
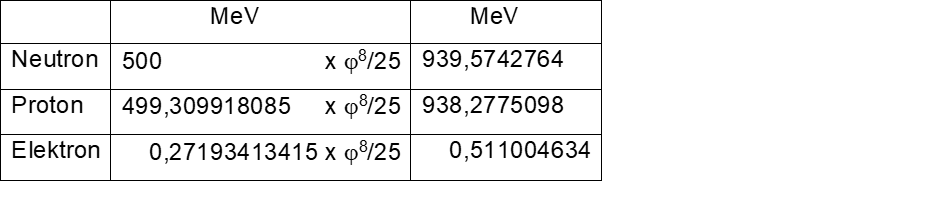
Die Ruhemassen der Elementarteilchen Kasten 9
Alle angeführten Zahlen liegen für die 1995er Werte innerhalb der zulässigen Grenzbereiche (siehe Kasten 3). Für die Daten des Jahres 2006 und 2022 sind sie ab der zweiten (Neutron) bzw. dritten (Proton, Elektron) Stelle hinter dem Komma etwas zu groß (siehe Kasten 4a und 4b).
Schließlich müssen die ermittelten MeV-Werte noch in die Einheit Kilogramm transferiert werden. Dafür benötigt man einen Umrechnungsfaktor (siehe Kasten 10).

Umrechnungsfaktor kg/MeV Kasten 10
Man sieht hier für die 1995er Werte Unterschiede ab der siebten Stelle hinter dem Komma, bei den 2006er Werten gibt es praktisch keine Unterschiede mehr. Bei den 2022er Werten ist der Umrechnungsfaktor ab der siebten Nachkommastelle etwas größer als bei den 2006er Werten, das Proton hat den größten Umrechnungsfaktor.
Ich habe mich damals (2006) für den Umrechnungsfaktor des Elektrons entschieden (1,78267581 x 10-30). Die vollständigen Werte für die drei Elementarteilchen Neutron, Proton und Elektron zeigt Kasten 11. In der letzten Spalte sind die Werte mit dem Umrechnungsfaktor des Jahres 2006 aufgeführt. Man muss sich allerdings fragen, wie genau eigentlich ein Wert angegeben sein sollte. Machen so viele Nachkommastellen wirklich Sinn? Für die Atomwissenschaft sicherlich. Kann man aber davon ausgehen, dass die Erbauer der Pyramiden wirklich zehn Nachkommastellen für die Massewerte der Elementarteilchen in ihre Bauwerke eincodieren wollten? Könnte es nicht viel mehr so sein, dass sie uns auf die glatte Zahl 500 für das Neutron aufmerksam machen wollten?

Die Ruhemassen der Elementarteilchen Kasten 11
Alle Tabellenwerte von Kasten 11 liegen innerhalb der genannten Grenzbereiche, wenn man die 1995er Daten heranzieht (vgl. Kasten 3). Rechnet man mit dem Umrechnungsfaktor für das Jahr 2006, so liegen die kg-Werte der letzten Spalte um eine Kleinigkeit unterhalb der unteren Grenzwerte (vgl. Kasten 4a). Für die Werte des Jahres 2022 gilt das gleiche wie für die Werte des Jahres 2006.
Ich glaube nicht, dass es bloßer Zufall ist, der es erlaubt, aus nur einer Verhältniszahl ( 1,00130416709 = Pyramidenfaktor ) recht genaue Werte für die Ruhemassen der Elementarteilchen zu berechnen.
Bei der Herleitung der Ruhemassen ist der Wert 0,03884773345 x φ8/25 MeV aufgetaucht. Er entspricht einem Siebtel der Ruhemasse des Elektrons. So beträgt dann die Ruhemasse eines Protons 1836 1/7 Elektronenmassen. Der Wert des Neutrons liegt bei 1838,680537 Elektronenmassen.
Der siebte Teil der Ruhemasse des Elektrons spielt eine ganz entscheidende Rolle. Das Auftauchen dieses Begriffs ( 1/7 mElektron ) hat mich veranlasst, das Periodensystem der Elemente genauer zu untersuchen. Herausgekommen dabei ist eine komplette Neueinteilung, die in den Grundzügen mit einer Figur in den Bergen von Palpa/Peru übereinstimmt – genau wie das von mir schon vorgestellte neue Modell des Atomkerns.
