Bogenminuten und allgemeine geometrische Formeln
Vergleich von π und πantik
Nachdem wir im letzten Kapitel verschiedene π – Werte kennengelernt haben, wollen wir den π am nächsten liegenden Wert πantik mit π vergleichen.
π = 3,141592654
πantik = 3,141640787
Die Differenz beträgt 4,813388 x 10-5. Mit was sollen wir rechnen, mit π oder mit πantik oder einem der anderen gefundenen π – Werte? Für πantik gibt es eine saubere geometrische Lösung.
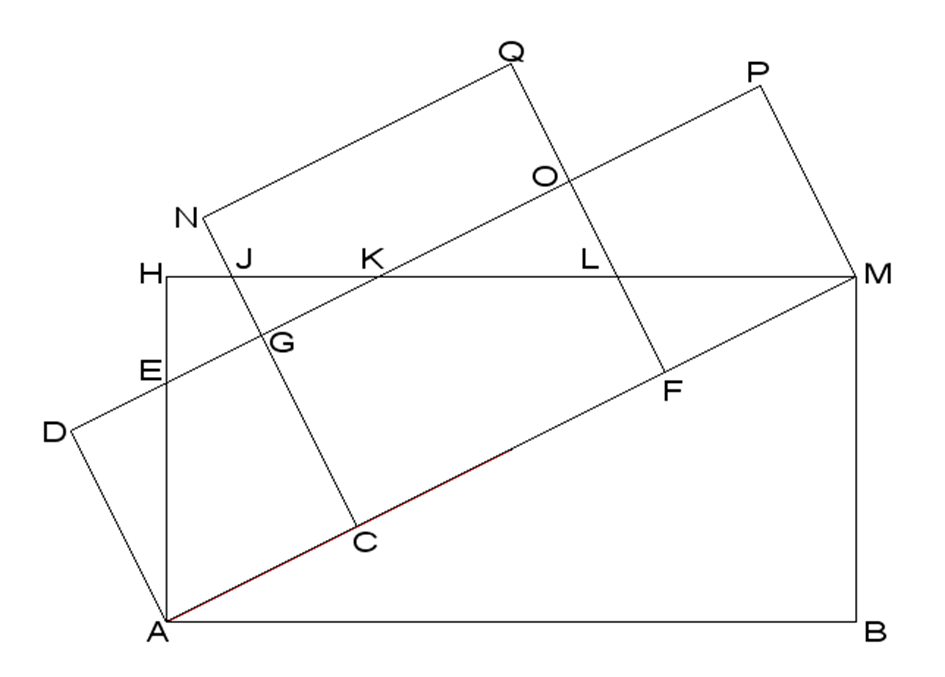
Abb.1: 2:1 – Rechteck mit den Quadraten auf der Diagonalen
Dazu betrachten wir Abb.1. Es handelt sich um das Doppelquadrat der Königskammer der Cheopspyramide mit den aus Kapitel 1 bekannten Quadraten auf der Diagonalen. Aus unserem System der fünf Maßeinheiten greifen wir nun die Heilige Elle (HE) heraus.
Es gilt: 1 HE = 0,636610018 m
Daraus folgt: 2 m = 3,141640787 HE = πantik HE
Es handelt sich um die Strecke GK in Abb.1. Hier liegt der Wert πantik in der Einheit HE direkt vor uns als gerade Strecke auf dem Boden der Königskammer. Das ist ein unumstößlicher geometrischer Tatbestand und in meinen Augen ein guter Grund unser bekanntes π durch πantik zu ersetzen.
Zwar hat Charles Funck – Hellet wie im Kapitel über die Königliche Elle beschrieben für das normale π bei König Salomos Tempel den Wert 6 für die Differenz von Umfang und Höhe der Säulen gefunden, jedoch glaube ich, dass die Strecke GK auf dem Boden der Königskammer der überzeugendere Beweis ist.
Der Unterschied zwischen Säulenumfang und Säulenhöhe ist zudem nur eine virtuelle Strecke. Außerdem ist der Meterwert für πantik in der Einheit KE ebenfalls 6. Das wirft auch einen Blick auf das sumerisch / babylonische Sexagesimalsystem, was in dieser Zahlenbeziehung sogar seinen Ursprung haben könnte.
Die Strecke Erde – Mond
Kann der winzige Unterschied von π und πantik eine Bedeutung haben? Die Entfernung Erde – Mond beträgt etwa 384 000 km. Dann beträgt der Umfang der Kreisbahn des Mondes um die Erde U = 2 π x 384 000 km = 2 412 743,158 km. Mit πantik zurück gerechnet beträgt der Radius r nur noch 383 994,117 km. Die Differenz ist 5,883 km. Dieser Unterschied kann von ausschlaggebender Bedeutung sein, wenn man eine Raumkapsel automatisch weich auf dem Mond landen will. Welcher der Radien bildet die Wirklichkeit besser ab?
Wenn die Erde eine ideale Kugel mit U = 40 000 000 m wäre, beträgt der Erdradius
rπ = 6366,197724 km
rπ-antik = 6366,100186 km
Differenz 97,538465 m
In der Größenordnung der Erdkugel beträgt die Radiendifferenz etwa 100 m, bei der Entfernung Erde – Mond bereits etwa 6 km!
Ich kann nicht entscheiden, ob π oder πantik die besseren Ergebnisse liefert.
Erdmaße
Da in πantik die Zahl φ2 und damit der Goldene Schnitt enthalten ist, der der gesamten Natur zu Grunde liegt, sollen – ausgehend von einer idealen Kugel – die Erdmaße mit π = πantik = 6/5 φ2 dargestellt werden:
Radius r = 6 366,100186 km
1 HE = 0,6366100186 m
Umfang U = 40 000 km
Fläche am Äquator A = 127 322 003,7 km2
Neigungswinkel der Cheopspyramide an der Basis
tan α = 1,273220037
Oberfläche O = 509 288 014,9 km2
Volumen V = 1,080726175 x 1012 km3
Wenn man in den geometrischen Formeln π durch πantik = 6/5 φ2 ersetzt, ergibt sich:
U = 2 x π x r = 2 x 6/5 φ2 x r → U = 12/5 x φ2 x r
Der Radius einer idealen Kugel mit dem Umfang 40 000 000 m beträgt
6 366 100,186 m, was 10 000 000 HE entspricht.
Der Vollkreis hat 360° oder 21 600 BM (BM = Bogenminute). 1 BM auf einem Kreis mit U = 40 000 000 m beträgt 1851,851852 m. Will man nun wissen, wie viele Bogenminuten der Radius dieses Kreises hat, muss man 6 366 100,186 m durch 1851,851852 m teilen. Das Ergebnis lautet 3 437,6941 BM.
6 366 100,186 m : 1851,851852 m = 3 437,6941 BM
Das lässt sich auch schreiben als: 3 437,6941 BM = 9000/φ2 BM.
Den Radius 9000/φ2 hat jeder Kreis und jede Kugel. Herleitung:
U [m] : 21600 = BM-Wert [m] → U = BM x 21600
U [m] : (2 x πa) = r [m] → U = r x 2 x πa
Das kann gleichgesetzt werden:
BM x 21600 = r x 2 x πa
r = BM x 21600 / (2 x πa) = BM x 10800 / πa =
= BM x 3437,6941 = BM x 9000 / φ2
Das ist die allgemeinste Form, den Radius eines Kreises oder einer Kugel auszudrücken und völlig unabhängig von irgendwelchen Maßeinheiten. Man muss nur den Bogenminutenwert der zur Anwendung kommenden Maßeinheit kennen und diesen mit 9000/φ2 multiplizieren. Im Bogenminutenwert der Maßeinheit steckt der betreffende Kreisumfang schon drin.
Beispiel idealisierte Erdkugel:
Umfang: 40 000 000 m
Bogenminutenwert: 1851,851852 m
Der Bogenminutenwert multipliziert mit 9000/φ2 ergibt den Radius zu
6 366 100,186 m.
Mathematiker arbeiten gerne mit dem Einheitskreis, dessen Radius definitionsgemäß r = 1 beträgt. Auf unsere Kugel übertragen heißt das für deren Umfang U = 2 x πantik x 1 = 6,283281574. Die Division durch 21 600 ergibt den BM – Wert zu 2,908926655 x 10-4 und der Reziprokwert davon ergibt 3437,694101 oder 9000/φ2.
Wenn der Bogenminutenwert einer Kugel bekannt ist, kann daraus sowohl ihr Umfang als auch ihr Radius berechnet werden.
U = BM x 21600
r = BM x 9000/φ2
Beispiel Mond:
1 BMMond = 0,5055… km
UMond = 0,5055… km x 21600 = 10 920 km
rMond = 0,5055… km x 9000/φ2 = 1 737,94535 km
Vorteile der Größenangabe in Bogenminuten
U = 21600 BM
Es kann jede beliebige Einheit verwendet werden (km, KE, HE, GE, außerirdische Maßeinheiten). Es muss lediglich ein Referenzmaß zur Eichung der Bogenminutenkurve bestehen. Im Fall von Kilometerangaben:
1 BMErde = 1,851851852 km
1 BMMond = 0,5055… km
Natürlich können auch alle anderen wichtigen geometrischen Parameter im Bogenminutensystem dargestellt werden.
Fläche am Äquator:
A = πa x r2 = 6/5 x φ2 x r2 =
= 6/5 x φ2 x ( 9000 / φ2 )2 = 6/5 x φ2 x 81 000 000 / φ4 =
= 97 200 000/φ2 = 37 127 096,28
Beispiel Erde:
A = 97 200 000 x 1,8518518522 km2 / φ2 = 333 333 334 km2 / φ2
= 127 322 003,7 km2
Oberfläche:
O = 4 x πa x r2 = 24/5 x φ2 x r2 = 24/5 x φ2 x (9000/φ2)2 =
= 24/5 x φ2 x 81 000 000 / φ4 = 388 800 000 / φ2 =
= 148 508 385,1
Beispiel Erde:
O = 388 800 000 x 1,8518518522 km2 / φ2 = 1 333 333 334 km2 / φ2
= 509 288 014,9 km2
Volumen:
Beim Volumen ergibt sich eine Besonderheit:
Die Volumenformel lässt sich auch schreiben als V = 4/3 x πa x r x r2. Der Term 4/3 x πa x r ergibt nach Ersetzen von πa und r die glatte Zahl 14 400:
4/3 x 6/5 x φ2 x 9000/ φ2 = 14 400
Das Volumen ergibt sich dann zu
V = 4/3 x πa x r x r2 = 14 400 x ( 9000/φ2 )2 =
= 14 400 x 81 000 000 / φ4 = 1,1664 x 1012 / φ4 =
= 1,701754662 x 1011
Beispiel Erde:
V = 1,1664 x 1012 x 1,8518518523 km3 / φ4 = 1,080726175 x 1012 km3
Zusammenfassung:
Die geometrischen Parameter Radius, Umfang, Fläche, Oberfläche und Volumen eines Körpers lassen sich ganz allgemein in der Einheit BM, BM2 und BM3 in Abhängigkeit von φ2 formulieren. Den Meterwert der genannten Parameter erhält man, wenn man die allgemeinen BM-Werte mit den speziellen BM-Werten der betreffenden Körper multipliziert.
rallg. = 9 000 / φ2 rspez. = rallg. x BM-Wert
Uallg. = 21 600 Uspez. = Uallg. x BM-Wert
Oallg. = 388 800 000 / φ2 Ospez. = Oallg. x BM-Wert2
Aallg. = 97 200 000 / φ2 Aspez. = Aallg. x BM-Wert2
Vallg. = 1,1664 x 1012 / φ4 Vspez. = Vallg. x BM-Wert3
Von der Bogenminute zum geodätischen Zoll
Der Vollkreis umfasst 360°. 1° besteht aus 60 Bogenminuten, 1 Bogenminute besteht aus 60 Bogensekunden. In Bogensekunden ausgedrückt hat der Vollkreis 360 x 60 x 60 = 1 296 000 Bogensekunden. Bezogen auf den Erdumfang von 40 000 000 m hat 1° = 111 111,11… m, 1 BM = 1 851,851852 m, 1 BS = 30,86419753 m.
1 Bogensekunde (BS) entspricht 100 geodätischen Fuß (geoF) und 1 geoF beinhaltet 12 geodätische Zoll (geoZ). Somit entspricht
1 geoF = 0,3086419753 m und
1 geoZ = 0,025720164 m.
Die Reziprokwerte von geodätischem Fuß und geodätischem Zoll sind:
1/geoF = 3,24 oder 1 m = 3,24 geoF
1/geoZ = 38,88 oder 1 m = 38,88 geoZ
Die Zahlenfolge 3888 ist in der allgemeinen Formel für die Oberfläche jeder Kugel enthalten. Gleichzeitig ist die Zahl 388 800 000 ein ganzzahliges Vielfaches von 9 000, von 21 600 und von 97 200 000.
Von der Kreisfläche zur Lichtgeschwindigkeit
1 Tag unserer Zeit hat 86 400 Sekunden (24 x 60 x 60). Der verstorbene Neuseeländer Bruce Cathie, ein ehemaliger Pilot und Erforscher von UFO – Routen auf der Erde, hat ein Gittersystem auf der Kugeloberfläche erfunden und parallel dazu eine Gitterzeit, indem er die normale Zeitsekunde mit 9/8 multipliziert und so die Gittersekunde (Gs) erhält.
1 s = 9/8 Gs
86 400 s = 9/8 x 86 400 Gs = 97 200 Gs.
Die Zahlenfolge 972 ist in der allgemeinen Formel für die Kreisfläche enthalten. Die Lichtgeschwindigkeit im Vakuum (c) beträgt idealisiert 300 000 000 m/s. Wandelt man die m in BM und die s in Gs um, erhält man c zu 144 000 BM/Gs.
300 000 000 / 1851,851852 = 162 000
162 000 / 9/8 = 144 000
Die Zahlenfolge 144 steckt wiederum im Term 4/3 x πa x r. Wie hieraus ersichtlich ist, hängt die Geometrie von Kugeln und Kreisen eng mit der Physik des Lichtes zusammen. Aber es geht noch viel weiter. In der allgemeinen Formel für die Oberfläche steckt der Term 4 x πa x r, also das dreifache von 14 400. Das ist 43200 und somit die Hälfte eines Erdentages in unseren normalen Zeitsekunden.
Cheopspyramide und Gitterzeit
Die Höhe der Cheopspyramide beträgt 280 KE. Teilt man das durch eine der Hauptpyramidenzahlen – nämlich 5,25 – erhält man die Zahl 53 1/3. Fasst man das als Zeitsekunde auf und multipliziert mit dem Umrechnungsfaktor 9/8, bekommt man punktgenau 60 Gs.
Die Höhe der Cheopspyramide steht also für 53 1/3 Zeit – oder 60 Gittersekunden. Die genaue Höhe der Chephrenpyramide ist bisher unbekannt, genau wie das planerische Prinzip, das dahintersteckt. Könnte es etwas mit der Gitterzeit zu tun haben?
Die Seitenlänge der Chephrenpyramide erhält man, wenn man von der Seitenlänge der Cheopspyramide (168 GE) an beiden Enden 5,25 GE abzieht zu 157,5 GE.
Laut Wikipedia beträgt ihre Höhe 143,87 m oder 275 KE (hier beträgt 1 KE 0,523163616 m). Die heutige Höhe sei laut einer Messung von Flinders Petrie aus dem Jahr 1880 136,40 m.
Ich will hier auf das planerische Prinzip abheben. Wenn die Höhe der Cheopspyramide für 60 GS steht, könnte die Höhe der Chephrenpyramide für 59 Gs stehen. Dies wären in KE zurück gerechnet 275 1/3 KE oder 144,17 m.
Die Höhendifferenz von Cheops – und Chephrenpyramide beträgt dann 4 2/3 KE. Teilt man 280 KE durch 60 Gs, bekommt man 4 2/3 KE/Gs. Multipliziert man 4 2/3 KE mit dem Umrechnungsfaktor 9/8, erhält man die Ausgangszahl unserer Rechnungen 5,25, diesmal nicht in der Einheit GE (Seitenlängen), sondern in der Einheit KE (Höhen).
Cheopspyramide und Lichtgeschwindigkeit
Die Koordinaten der Cheopspyramide sind:
29°58´45„ N und 31°8`2„ O (Quelle Wikipedia)
29°58`44,383„ N und 31°7`57,0194„ O (Quelle GPMP)
29°58´45„ = 29,97916667°
29°58`44,383„ = 29,97899528°
Fasst man den nördlichen Breitengrad der Cheopspyramide als Dezimalzahl auf, ergibt sich ein zahlenmäßiger Bezug zur Vakuumlichtgeschwindigkeit (c = 299792,458 km/s), wobei die Angabe aus Wikipedia näher als die von GPMP liegt (GPMP = Giza – Plateau – Mapping – Project).
Fasst man c als Koordinate im Dezimalsystem auf, kommt man im Bogengradsystem auf 29°58`45,28„als Pyramidenmittelpunkt. Der Unterschied von 28„ entspricht etwa 8,64 m. Die östliche Länge der Pyramide könnte dann als Nullmeridian analog zum Greenwich – Nullmeridian aufgefasst werden.
Gittersystem der Erde
Man kann die Erdoberfläche (388 800 000/φ2) einteilen in 6 Quadrate und 8 gleichseitige Dreiecke. 1 Quadrat besteht aus 4 Kugeldreiecken.
Flächeninhalte:
Quadrat 43 200 000/φ2
Kugeldreieck 10 800 000/φ2
Gleichseitiges Dreieck 16 200 000/φ2
6 Quadrate 259 200 000/φ2
8 gleichseitige Dreiecke 129 600 000/φ2
Summe 388 800 000/φ2
Bei dieser Einteilung bekommt man Zahlenbezüge (Resonanzen?) zur halben Tageslänge (43 200 000) und zur Anzahl der Bogensekunden eines Kreises (129 600 000).
Betrachtet man z.B. die Diagonalen eines Quadrats in der Ebene und auf der Kugeloberfläche, so muss man in der Ebene die Grundseite mit √2 multiplizieren, auf der Kugeloberfläche dagegen mit 1,5. Der Quotient 1,5 geteilt durch √2 ergibt √(9/8) und ist damit resonant zum Umrechnungsfaktor von Zeitsekunden in Gittersekunden (9/8).
Der Weg zur Elementarladung und zur Elektrizität
300 000 000 m/s für die Lichtgeschwindigkeit c und 40 000 000 m für den Erdumfang sind nicht die genauen Werte, sondern es sind „idealisierte Werte“. Lässt man das auch für die Avogadrosche Zahl NA, für die Faraday-Konstante F und für die Elementarladung e– gelten, ergeben sich weitere Zusammenhänge.
Die genauen Zahlenwerte sind:
NA = 6,02214129(27) x 1023 mol-1 = F/e
F = 96 485,3365(21) C/mol
e– = 1,602176565 x 10-19 C
Im idealisierten Zahlensystem gilt:
NA = 6 x 1023 mol-1
F = 96 000 C/mol
e– = 1,6 x 10-19 C
Daraus ergibt sich das Coulomb (C) zu
1 C = 1 A x s = 1/(1,6 x 10-19 e–) x s = 6,25 x 1018 e– x s
Und daraus
1 A = 1 C/s = 6,25 x 1018 e–/s
Bei einer Stromstärke von 1 A fließen 6,25 x 1018 elektrische Ladungsträger (Elementarladungen = Elektronen) pro Sekunde.
Nach Umwandlung von Sekunden in Gittersekunden gilt:
1 GA = 1 C/Gs = 8/9 x 6,25 x 1018 e–/Gs = 5 5/9 x 1018 e–/Gs
1 GA2 = 3,086419753 x 1037 e-2/Gs2
Da 1 geoF = 0,3086419753 m ist das GA2 in der Zahlenfolge identisch mit dem geodätischen Fuß. Über die Zahl 12 ist es auch mit 1 geoZ = 0,025720164 m verbunden und da 12 x 12 = 144 auch mit der Zahlenfolge des Wertes für die Vakuumlichtgeschwindigkeit.
In 1 Gs fließen 50/9 x 1018 Elektronen, in 97 200 Gs fließen 5,4 x 1023 Elektronen. Der Kehrwert davon beträgt1,851851852 x 10-24. Die Zahlenfolge 1851851852 weist auf die Bogenminute hin. Somit sind Gittertag (Zeit) und Elektrizität (A) mit der Entfernung (BM) auf der Erde gekoppelt.
1 astronomische Einheit (AE) beträgt genau 149 597 870 700 m. Idealisiert man diesen Wert ebenfalls, ergibt sich:
1 AE = 150 000 000 000 m = 81 000 000 BM = 4 860 000 000 BS =
= 4,86 x 1011 geoF = 5,832 x 1012 geoZ
Überraschenderweise steckt der Wert 81 000 000 BM auch in der allgemeinen Formel für das Volumen:
V = 4/3 x πa x r x r2 = 14 400 x 81 000 000/φ4 = 1,1664 x 1012/φ4
In der Volumenformel verstecken sich somit die Zahlenfolgen für die Vakuumlichtgeschwindigkeit und die Entfernung Erde – Sonne.
Diskussion
Was lässt sich nun mit diesen Erkenntnissen anfangen?
Die ägyptische Königselle wurde nach geometrischen Prinzipien geschaffen und steht über die Zahl φ2 mit den Proportionen des Goldenen Schnitts im Zusammenhang. Der Goldene Schnitt wiederum liegt der gesamten Natur unseres Planeten Erde und wahrscheinlich auch des Sonnensystems zugrunde.
Die Cheopspyramide erweist sich somit als steinernes mathematisch-naturwissenschaftliches Lehrbuch. Im Licht der hier extrahierten mathematischen Erkenntnisse ist es m.E. extrem unwahrscheinlich, dass die Ägypter um 2500 v.Chr. die Erbauer dieser Pyramide waren. Keinesfalls war damals eine solch hoch entwickelte Mathematik mit Irrationalzahlen bekannt.
Eine praktische Anwendung der ägyptischen Königselle könnte die Kreisberechnung vereinfachen:
Ganzzahlige Radien in der Einheit Meter ergeben ganzzahlige Kreisumfänge in der Einheit KE. Beispiel: r = 2 m, U = 2 x pi-antik x 2 m = 2 x (6/5) φ2 x 2 x 5/φ2 KE = 24 KE.
Diese Rechnung zeigt, dass unser allgemein bekanntes pi durch pi-antik ersetzt werden könnte.
Die Tatsache, dass pi-antik in der Einheit Meter zur glatten Zahl 6 in der Einheit KE wird, wirft auch ein neues Licht auf das sumerisch-babylonische Sexagesimalsystem, was ja ebenfalls auf der Zahl 6 basiert und den Vollkreis von 360° in 6 Teile zu je 60° unterteilt.
Und noch etwas ist höchst interessant: Der Wert für die Irrationalzahl φ2 in der Einheit Meter wird in der Einheit KE (königliche Elle) zur glatten Zahl 5.
