Das Pyramidenfeld von Gizeh und die ägyptische königliche Elle
Im Buch „Der Pyramiden – Code“ befindet sich ein Lageplan des Pyramidenfeldes von Gizeh, aus dem die Lage der drei großen Pyramiden hervorgeht
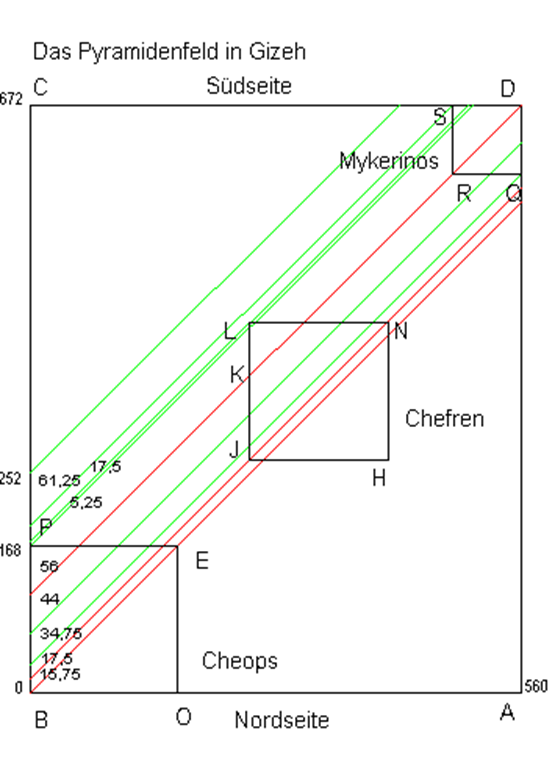
Die Cheopspyramide befindet sich in der Nordostecke, die Mykerinospyramide in der Südwestecke des Feldes. Dazwischen in der Mitte steht die Chefrenpyramide. Die Maßeinheit im Lageplan ist die GE (Grundeinheit). Sie ist eine der Maßeinheiten, die sich nach der Entdeckung der genauen Größe der ägyptischen königlichen Elle (KE) ergab.
Die ägyptische königliche Elle (KE)
Nach der Rückkehr von meiner ersten Ägyptenreise 1997 stellte sich mir als erstes die Frage, wie lang genau das den Bauwerken zu Grunde liegende Maß der ägyptischen königlichen Elle war. Die Ägyptologie geht von einem Näherungswert von 52,5 cm aus.
Um diese Frage beantworten zu können, stellte ich zusammen, was in der Maßeinheit KE bereits bekannt und von der Ägyptologie anerkannt war:
Cheopspyramide:
Höhe 280 KE
Länge einer Grundseite 440 KE
Königskammer Cheopspyramide:
Länge 20 KE
Breite 10 KE
Daneben gibt es noch Überlieferungen. In Al Makrizis Hitat, einer Reihe von arabischen Berichten aus dem frühen Mittelalter, wird an mehreren Stellen behauptet, die Höhe der Cheopspyramide entspreche ihrer Grundseitenlänge. Dass dies so nicht stimmt, kann man vor Ort schon mit bloßem Auge sehen. Da Überlieferungen aber auch einen wahren Kern haben können, sollte man diese Behauptung nicht von vornherein als Unsinn abtun.
Eine weitere Überlieferung stammt von Herodot: Das Quadrat über der Höhe der Cheopspyramide sei flächengleich mit zwei ihrer Oberflächendreiecke.
Weiterhin existieren Vermutungen aus der Moderne. Eine davon lautet: Der Umfang der Cheopspyramide geteilt durch ihre doppelte Höhe ergibt die Zahl π.
Ich stellte mir die Frage: Was wäre, wenn es mit Hilfe des genauen Wertes für die KE gelänge, diese beiden Überlieferungen und obige Vermutung aus der Moderne zu verifizieren und was das für Auswirkungen auf unser heutiges Weltbild hätte. Umgekehrt könnte das natürlich auch die Richtigkeit des gefundenen Wertes für die KE bestätigen.
Zunächst aber muss man einen geeigneten Ansatz finden, um die KE – Werte in die Einheit Meter umrechnen zu können. Messungen sind problematisch. Will man die Grundseitenlängen der Cheopspyramide messen, stellt man fest, dass die Ecksteine am Boden fehlen. Die dennoch messtechnisch ermittelten Werte zeigen, dass alle vier Grundseiten verschieden lang sind. Außerdem fehlt größtenteils die Außenverkleidung, so dass es äußerst schwierig ist, geeignete Messpunkte festzulegen. Zu allem Überfluss hat 1301 n.Chr. ein Erdbeben große Teile Kairos zerstört. Bei diesem Ereignis verloren die drei Pyramiden ihre Verschalungen. Das hat zu dem Spruch geführt: „Der Mensch fürchtet die Zeit, die Zeit fürchtet die Pyramiden.“
Der heute wissenschaftlich akzeptierte Wert für die Länge einer Grundseite der Cheopspyramide beträgt 230,36 m. Teilt man nun 230,36 m durch 440 (KE – Wert einer Grundseite), erhält man 0,523545 m oder 52,3545 cm. Das ist etwas weniger als der Näherungswert von 52,5 cm der Ägyptologie.
Charles Funck – Hellet, ein französischer Mathematiker, vertrat die Ansicht, die beim biblischen Tempelbau Salomos verwendete Elle könne nur die ägyptische Königselle gewesen sein. Salomo beauftragte Hiram, den Tempel in Jerusalem so zu bauen, dass dessen Säulen 18 Ellen hoch sein und ihr Umfang 12 Ellen betragen sollten. Dann entspricht eine Elle dem zwölften Teil des Umfangs und somit 30° des Kreisbogens. Das wiederum entspricht π/6, da in der Mathematik 360° 2 x π entsprechen. Der Unterschied zwischen Höhe und Umfang der Säulen beträgt in einer geraden Linie 6 Ellen und das sei genau π. Deshalb legte Funck – Hellet die Elle zu π/6 m = 52,3598775 cm fest. Das war erstmals ein rein mathematischer Ansatz zur Bestimmung des Meterwertes für eine ägyptische königliche Elle. Funck – Hellets Ansatz stammt aus dem Jahr 1952 und geht auf die Bibel zurück. Damit hält er wissenschaftlichen Kriterien nicht stand und fällt in den Bereich Pseudo – Mathematik. Ist die Verknüpfung von Cheopspyramide und Bibeltext überhauptsinnvoll? Wie sich noch zeigen wird, kann diese Frage eindeutig mit ja beantwortet werden.
Multipliziert man nun 440 mit π/6 erhält man 230,38 m für die Länge einer Grundseite, tut man dies mit 280 erhält man 146,61 m für die Pyramidenhöhe.
Wenden wir uns nun der Königskammer in der Cheopspyramide zu. Deren Länge beträgt bekanntlich 20 KE, ihre Breite 10 KE. Sie ist also ein Doppelquadrat. Im Gegensatz zu den Grundseiten der Pyramide lassen sich Länge und Breite der Königskammer sehr genau messen. In der Einheit Meter beträgt ihre Länge 10,47 m und ihre Breite 5,23 m. Es fällt auf, dass hier für die Länge 1 cm zu viel gemessen wurde. Ist die Königskammer also doch kein exaktes Doppelquadrat? Oder ist der angesetzte Wert von 52,3 cm für die KE nicht exakt genug?
Wir können an Hand der Königskammerwerte versuchen, einen oberen und einen unteren Grenzwert für 1 KE zu definieren.
10,47 m geteilt durch 20 KE ergibt 0,5235 m/KE. 5,23 m geteilt durch 10 ergibt 0,523 m/KE. Wie wirken sich aber äußere Einflüsse wie Erdbeben und das große Gewicht der Steinblöcke auf Kammerlänge und – breite aus?
Kleiner kann die Kammer eigentlich nicht geworden sein, nur größer. Geht man bei gemessener Kammerbreite von einer Toleranz von 3 cm aus, ergibt sich für 1 KE ein unterer Grenzwert von 0,52 m.
Bei den Kammermaßen können auch Rundungsfehler auftreten. Die heute gemessene Länge beträgt 10,47 m. Unterschiede von 1 cm und 1 mm sind optisch erkennbar, Unterschiede im Zehntelmillimeterbereich aber nicht mehr. Fügt man als Toleranz 1 cm zu den gemessenen 10,47 m hinzu (10,48 m), erhält man einen oberen Grenzwert von 0,524 m.
Die Königselle sollte sich also zwischen 52 cm und 52,4 cm bewegen. Die Differenz beträgt 4 mm. Der Näherungswert der Ägyptologie (52,5 cm) ist somit wirklich nur ein Näherungswert.
Wie wirken sich die definierten Grenzwerte auf Höhe und Grundseitenlänge der Cheopspyramide aus?
Als Referenzwerte dienen die von Funck – Hellet abgeleiteten Meterwerte 146,61 m für die Höhe und 230,38 m für die Länge einer Grundseite. Multipliziert man 280 KE mit 0,52 (unterer Grenzwert) bekommt man als Höhe 145,60 m. Das ist eindeutig zu niedrig. Im Fall von 0,524 ergeben sich als Höhe 146,72. Das ist etwas zu hoch. Der 4 mm betragende Unterschied zwischen unterem und oberem Grenzwert summiert sich im Fall der Pyramidenhöhe zu einer Differenz von 1,12 m auf.
Führt man dieselbe Rechnung für die Länge einer Grundseite durch, ergibt sich für den unteren Grenzwert 228,30 m, das ist zu kurz. Für den oberen Grenzwert erhält man 230,56 m, das ist etwas zu lang. Die Differenz beträgt hier sogar 1,76 m.
Setzt man die berechneten Werte zu den Referenzwerten in Beziehung, erkennt man, dass der wahre Wert für eine KE näher an 0,524 m liegen dürfte als an 0,52 m.
Wir haben nun einen oberen und einen unteren Grenzwert für 1 KE und Funck – Hellets mathematischen Ansatz, nämlich π/6 zu 52,3598775 cm. Jetzt benötigen wir einen eigenen Ansatz, um das Problem der ägyptischen königlichen Elle lösen zu können. Hier ist mir die Geometrie zu Hilfe gekommen.
Wir betrachten die Königskammer der Cheopspyraide mit der eingezeichneten Diagonale AC (siehe Abb.2). Nach dem Satz des Pythagoras errechnet sich die Länge der Diagonale zu √500 KE = 10 x √5 KE, die halbe Diagonale AM = MC zu 5 x √5 KE = 11,18033989 KE.
√5 wiederum hat eine wohl definierte Beziehung zur Naturkonstante φ (phi):
√5 = φ + 1/φ = 2,236067977. In Zahlen ausgedrückt: 1,618033989 + 0,618033988 = 2,236067977. Was ist das Besondere an φ? φ steht für den Goldenen Schnitt.
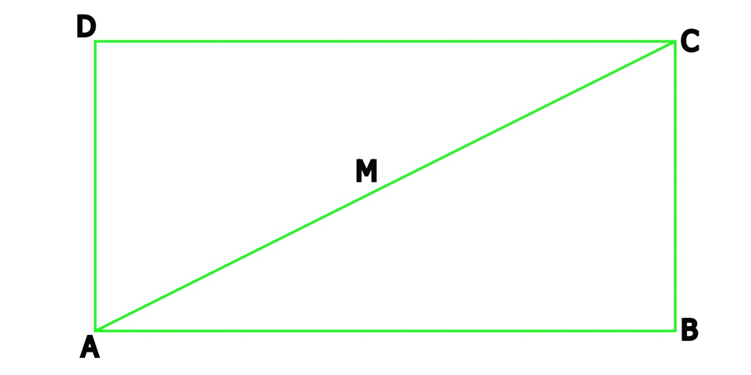
Der Kehrwert von φ (1/φ) beträgt 0,618, φ selbst 1,618 und φ2 2,618. In der gesamten Zahlenwelt ist dies die einzige Stelle, wo Kehrwert und Quadrat einer Zahl sich um genau die Zahl 1 unterscheiden. Es werden nun Quadrate auf der Diagonalen errichtet.
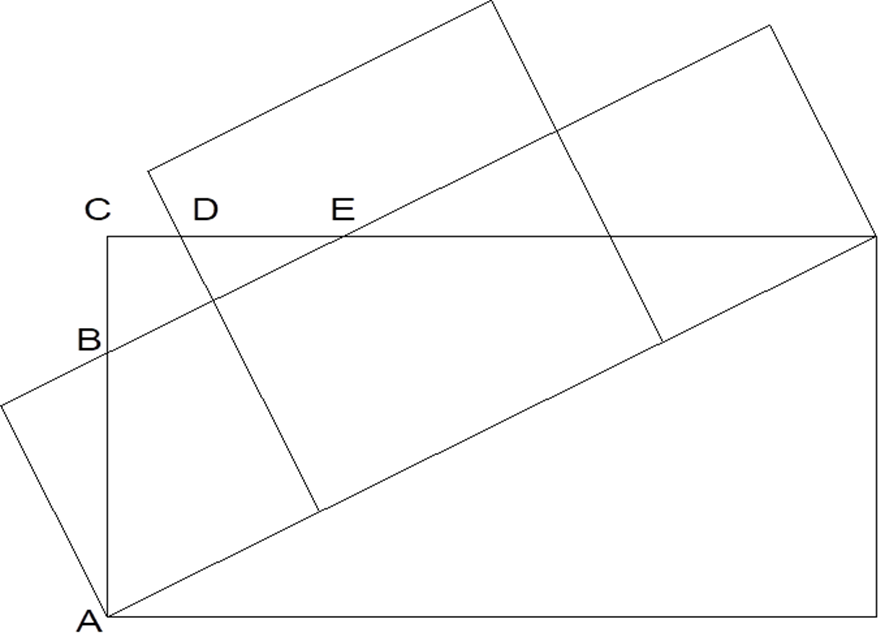
Auf der Diagonalen befinden sich dann zwei kleinere äußere Quadrate und ein größeres inneres Quadrat. Wir wissen, dass die Diagonalenlänge 10 x √5 KE = 22,36067978 KE beträgt. Die Seitenlänge des mittleren größeren Quadrats beträgt 10 KE. Wenn wir die von der Diagonalenlänge abziehen, erhalten wir 12,36067978 KE. Die Division durch 2 ergibt 6,180339888 KE = 10/φ KE und ist die Seitenlänge der beiden äußeren kleineren Quadrate auf der Diagonalen.
Die Seitenlängen der Dreiecke in der Figur, die miteinander den rechten Winkel bilden sind alle halb bzw. doppelt so groß. Bekanntlich beträgt die Kammerlänge 20 KE, die Kammerbreite 10 KE. Wir wollen nun die einzelnen Strecken AB, BC, CD und DE betrachten.
Die Seitenlänge des linken äußeren kleineren Quadrats beträgt von Punkt A ausgehend 10/φ KE. Die zweite Dreieckseite zum Punkt B beträgt die Hälfte, also 5/φ KE. Nach dem Satz des Pythagoras kann man die Strecke AB ausrechnen, sie beträgt 6,909830055 KE. Rechnet man diesen KE – Wert nach Funck – Hellet durch Multiplikation mit π/6 in die Einheit Meter um, erhält man 3,617978556 m. Diese Zahl erinnert an 3,618033989, das ist φ + 2.
Die Strecke BC beträgt 10 KE – 6,90983005 KE = 3,09016995 KE. Die Multiplikation mit π/6 ergibt 1,618009202 m. Das erinnert an φ = 1,618033989.
Für die Strecke CD erhält man einen Meterwert von 0,999984678 m. Hier ist die 1 ganz nah.
Die Strecke DE ergibt 2,236033718 m, dies erinnert an √5 = 2,236067977.
Ich habe mich nun gefragt, ob es statt π/6 einen anderen Umrechnungsfaktor gibt, der die genauen Werte φ + 2, φ, 1 und √5 liefert.
Die Antwort ist ja. Der neue Umrechnungsfaktor ist φ2/5 zu 52,3606797 cm. Damit ist die ägyptische königliche Elle auf mathematischem Weg eindeutig identifiziert.
Multipliziert man nun diesen Wert mit 6, erhält man den in der Nähe von π liegenden Wert 6/5 φ2 = 3,141640787. Eingedenk der alten Baumeister habe ich diesen Wert π – antik genannt.
Die Unterschiede sind sehr gering:
| π – antik = 3,141640787 | 1/5 φ2 = 0,523606797 |
| π = 3,141592654 | 1/6 π = 0,523598775 |
Die Werte unterscheiden sich erst ab der vierten Nachkommastelle.
Wo steckt nun der fehlende Zentimeter in der Königskammer?
Durch Messungen ermittelt wurde die Kammerlänge zu 10,47m und die Kammerbreite zu 5,23 m. Mit dem neuen Umrechnungsfaktor φ2/5 beträgt die Kammerlänge 10,47213596 m, die Kammerbreite 5,23606798 m. Auf drei Stellen hinter dem Komma genau sind dies 10,472 m und 5,236 m. Die Königskammer ist also doch ein echtes Doppelquadrat.
Tabelle 1 zeigt die zusammengefassten Werte für beide Umrechnungsfaktoren.
| π/6 | φ2/5 | |
| Breite | 5,235987756 m | 5,236067979 m |
| Länge | 10,47197551 m | 10,47213596 m |
| Diagonale | 11,70802455 m | 11,70820394 m |
| Seite Kleineres Quadrat | 3,236018397 m | 3,236067978 m |
Sowohl mit π/6 als auch mit φ2/5 bewegt man sich innerhalb der gleichen geometrischen Figur. Aber nur und ausschließlich mit φ2/5 sind die Seitenlängen der Kammer (10 KE und 20 KE) in der Einheit Meter punktgenaue Vielfache von φ2 (2 φ2 und 4 φ2).
Die Umwandlung von KE in m über den Umrechnungsfaktor 1/5 φ2 ist die einzig existierende Lösung für das Doppelquadrat der Königskammer in der Cheopspyramide, das für die Strecken AB, BC, CD und DE die dargestellten Ergebnisse liefert.
Mit allen anderen Umrechnungsfaktoren, die gewählt werden könnten, ergeben sich bestenfalls Näherungswerte (siehe π/6).
Die Lösung ist eindeutig. Deshalb muss der genaue Meterwert der ägyptischen königlichen Elle zu 1/5 φ2 = 0,523606797 m festgesetzt werden.
Was ist das Besondere an der Einheit KE gegenüber dem Meter?
| 1/5 φ2 | 0,523606797 m | 1 KE |
| 5/5 φ2 | 2,618033989 m | 5 KE |
| 6/5 φ2 | 3,141640787 m | 6 KE |
| 10/5 φ2 | 5,23606797 m | 10 KE |
Die ägyptische königliche Elle besteht somit aus Vielfachen von 1/5 φ2 m, und damit steckt in der Einheit KE die Naturkonstante φ bereits drinnen. Aber nicht als φ selbst, sondern als deren Quadrat. Im mathematischen Unterricht in der Schule war immer nur von φ als dem Goldenen Schnitt die Rede. φ2 kam darin höchst selten vor. Wie sich noch zeigen wird, war für die Erbauer der Pyramiden von Gizeh φ2 die wichtigere Zahl.
Nehmen wir jetzt einmal die moderne Vermutung unter die Lupe, der Umfang der Cheopspyramide geteilt durch ihre doppelte Höhe ergebe die Zahl π. Der Umfang beträgt 4 x 440 KE = 1760 KE. Die doppelte Höhe beträgt 2 x 280 KE = 560 KE. 1760 KE geteilt durch 560 KE ergibt 3 1/7 = 3,142857143. Das liegt zwar in der Nähe von π, ist aber nicht π selbst.
Das Basisdreieck der Cheopspyramide
Das Basisdreieck der Cheopspyramide geht von ihrem Mittelpunkt am Boden aus. Die längere Dreieckseite ist die Höhe h = 280 KE, die kürzere ist wieder vom Mittelpunkt ausgehend die Länge einer halben Grundseite ½ s = 220 KE. Diese beiden Dreieckseiten heißen in der Mathematik Katheten. Deren Verhältnis zueinander bezeichnet man als Tangens. 220 KE geteilt durch 280 KE ergibt 0,785714285. Multipliziert man diese Zahl mit 4, ergibt sich 3 1/7 = 3,142857143.
Wir haben jetzt die Formel gefunden: ¼ π – Wert entspricht der halben Seitenlänge geteilt durch die Pyramidenhöhe (¼ π – Wert = ½ s : h).
Löst man das nach ½ s auf, ergibt sich eine weitere Formel: ½ s = ¼ π – Wert x h.
Führt man die Rechnung nach dieser Formel für π – antik durch, erhält man für die halbe Grundseitenlänge 219,9148551 KE. Wir haben jetzt zwei unterschiedliche Werte für die halbe Grundseitenlänge, nämlich 220 KE (3 1/7 – System) und 219,9148551 KE (π – antik – System). Könnte hier ansatzweise die Erklärung für die von der Ägyptologie festgestellten vier unterschiedlichen Grundseitenlängen der Cheopspyramide stecken? Dann müsste es noch zwei weitere unterschiedliche π – Systeme geben.
Ein weiterer π – Wert (π – phi)
Betrachten wir einmal die Schnittpunkte der Cosinus – Tangens – und der Sinus – Cotangens – Kurven. Da jedes Dreieck drei Winkel zwischen seinen Seiten besitzt und in einem rechtwinkligen Dreieck ein Winkel mit 90° bereits feststeht, bleiben zwei Winkel übrig (α und β).
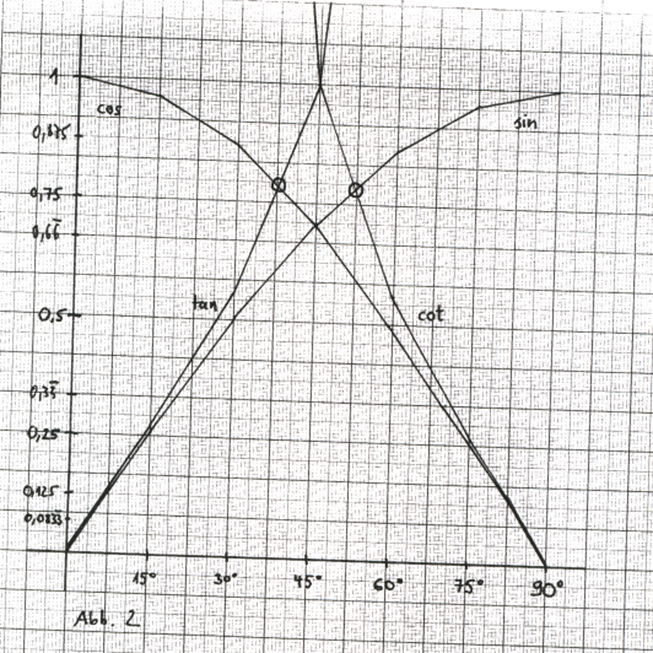
Für alle möglichen rechtwinkligen Dreiecke ergeben sich für die verschiedenen Winkelverhältnisse (Sinus, Cosinus, Tangens, Cotangens) verschiedene Werte, die sich in Form von vier Kurven darstellen lassen (siehe Abb.4). Dabei ergeben sich zwei Schnittpunkte für die vier Kurvenverläufe.
Für einen Winkel α = 51,82729238° erhält man sin α = cot α = 0,786151377.
Für einen Winkel β = 38,17270762° erhält man cos β = tan β = 0,786151377.
Beide Winkel (α und β) ergeben zusammen 90°.
Man kann den Wert 0,786151377 als ¼ π – Wert auffassen und nach Multiplikation mit vier steht dann 3,144605511. Ich habe dieswen Wert π – phi genannt.
Wenden wir nun die Formel ½ s = ¼ π – Wert x h an, erhalten wir eine dritte halbe Grundseitenlänge von 220,1223856 KE.
Dass π – phi von φ abstammt, verdeutlichen die Tangenswerte für das Oberflächendreieck der Cheopspyramide:
Tangenswert des Winkels an der Pyramidenspitze: 0,618033989 = 1/φ.
Tangenswert des Winkels an der Pyramidenbass: 1,618033989 = φ.
Herodots Überlieferung
Da hier das Oberflächendreieck der Cheopspyramide auftaucht, liegt es nahe, Herodots Überlieferung zu prüfen: Das Quadrat über der Pyramidenhöhe sei flächengleich mit zwei ihrer Oberflächendreiecke (h2 = 2 x OFD).
Die Berechnung von h2 ist einfach: 280 KE x 280 KE = 78 400 KE2.
Ein Oberflächendreieck (OFD) besteht aus der Seitenhöhe der Pyramide (sh = Linie von der Pyramidenspitze entlang der Pyramidenoberfläche zur Mitte einer Grundseite am Boden), der halben Grundseitenlänge ( ½ s = Linie von der Mitte einer Grundseite am Boden zur Pyramidenecke am Boden) und der Polkante (p = Linie von der Pyramidenecke am Boden entlang ihrer Oberfläche zur Pyramidenspitze).
Die Seitenhöhe sh und die halbe Grundseite ( ½ s) bilden die Hälfte eines Rechtecks, wobei die Polkante p zur Diagonale dieses Rechtecks wird. Die Fläche eines Rechtecks ergibt sich aus der Multiplikation seiner beiden Grundseiten, also Seitenhöhe mal halbe Grundseitenlänge (Fläche 2 x OFD = sh x ½ s).
Die halbe Grundseitenlänge im π – phi – System ist bekannt (220,1223856 KE), berechnet werden muss noch die Seitenhöhe. Diese ist als Hypotenuse Bestandteil des Basisdreiecks h, ½ s und sh. Da h und ½ s bekannt sind, errechnet sich sh nach dem Satz des Pythagoras zu sh = 356,1655019 KE.
Jetzt können wir die Multipliktion sh x ½ s durchführen und bekommen als Ergebnis 78 400 KE2. Hiermit ist bewiesen, dass Herodots Überlieferung genau stimmt.
Tabelle 3 zeigt eine Übersicht über die bisher gefundenen drei π – Systeme.
| π – Wert | 2 x OFD | h2 / 2 x OFD |
| 3 1/7 | 78 339,77 KE2 | 1,008 |
| π – antik | 78 297,89 KE2 | 1,0013 = m N/P |
| π – phi | 78 400 KE2 | 1,0000 |
Herodots Überlieferung stimmt für das π – phi – System genau. Für das π – antik – System führt der Weg direkt in die Atomphysik, denn der Wert 1,0013 ist das genaue Massenverhältnis eines Neutrons zu einem Proton, den beiden Bestandteilen aller Atomkerne.
Eine neue grundlegende Einheit
Nach der Formel ¼ – π – Wert x h = ½ s kann man die ganze Länge einer Grundseite berechnen, wenn man beide Seiten der Formel mit zwei multipliziert. Dann ergibt sich s = ½ π – Wert x h. Tabelle 4 zeigt die Seitenlängen in den verschiedenen π – Systemen.
| π – Wert | Seitenlänge |
| π | 439,8229715 KE |
| 3 1/7 | 440 KE |
| π – antik | 439,8297102 KE |
| π – phi | 440,2447715 KE |
Im π – antik – System beträgt die Grundseitenlänge 439,8297102 KE. Teilt man diese Zahl durch φ2, erhält man die glatte Zahl 168. Damit ist eine neue Maßeinheit herausgefunden, die Grundeinheit (GE), die dem gesamten Pyramidenfeld von Gizeh zu Grunde liegt. Im π – antik – System beträgt die Länge einer Grundseite also 168 GE.
Betrachten wir nochmals Abbildung 1, das Rechteck des Pyramidenfeldes von Gizeh. Die lange Seite des Rechtecks beträgt 672 GE, was dem Umfang der Cheopspyramide entspricht. Die kurze Seite ist 560 GE lang. Die Grundseite der Cheopspyramide beträgt wie dargelegt 168 GE, die der Chefrenpyramide beträgt 157,5 GE und die der Mykerinospyramide beträgt 78,75 GE.
Phi und seine Zahlenfamilie
Phi (φ) ist die Basiszahl für den Goldenen Schnitt und steht somit für harmonische Proportionen. Die gesamte Natur ist nach den Proportionen des Goldenen Schnitts aufgebaut.
1/φ = 0,618033989
φ = 1,618033989
φ2 = 2,618033989
φ2 ist die wichtigste Zahl in der Pyramiden – Mathematik.
Wie teilt man eine Strecke nach dem Goldenen Schnitt?
Strecke geteilt durch φ ergibt den größeren Teil der Strecke.
Strecke geteilt durch φ2 ergibt den kleineren Teil der Strecke.
Als Formel ausgedrückt kann man schreiben, wenn die Streckenlänge 1 beträgt:
1/φ + 1/φ2 = 1
Wenn die Strecke 1 m betägt, ist der größere Teil 0,618 m lang und der kleinere Teil 0,382 m.
Man kann den Goldenen Schnitt noch erweitern, indem man die Gesamtstrecke in die Verhältnisse einbezieht: Die Gesamtstrecke verhält sich zum größeren Teil wie der größere zum kleineren.
Als Formel geschrieben: 1 : 1/φ = 1/φ : φ2
Was ist das Besondere an der Einheit GE? Mit der Teilung durch φ2 wird die ganze Strecke resonant zum kleineren Teil. Die Grundseitenlänge der Cheopspyramide beträgt im π – antik – System 439,8297103 KE. Die Teilung durch φ2 ergibt 168 KE, die wiederum resonant sind zu 168 GE. Damit steckt der Goldene Schnitt in jeder Strecke, wenn man sie durch φ2 teilt.
Eine weitere Maßeinheit: Heilige Elle (HE)
Wir begeben uns nun auf eine höhere Ebene und betrachten die idealisierten Erdmaße. Der Erdumfang beträgt idealisiert 40 000 000 m. Um den idealisierten Radius zu bekommen, muss man durch 2 x π teilen. Wir wollen hier aber π – antik verwenden. Dann ergibt sich der Erdradius zu 6 366 100,186 m. Teilt man diese Zahl durch 10 000 000 erhält man die Heilige Elle zu 0,6366100186 m. Dieser Wert entspricht 2/π – antik. Der Meterwert für die HE beträgt 1 m = 1,570820394 HE = ½ x π – antik. In der Maßeinheit HE steckt π – antik in Form des Umrechnungsfaktors 3/5 φ2 bereits drinnen. Multipliziert man den Wert 1 HE = 0,6366100186 mit zwei, bekommt man 1,273220037. Das ist der Tangenswert des Neigungswinkels an der Basis der Cheopspyramide im π – antik – System.
Nachdem wir jetzt die Maßeinheit Heilige Elle (HE) definiert haben, wollen wir uns an die eigentlich unmögliche Behauptung aus Al Makrizis Hitat erinnern: Die Seitenlänge der Cheopspyramide ist genau so groß wie die Höhe der Pyramide.
Die Grundseitenlänge beträgt im π – antik – System 230,2978262 m, die Höhe 146,6099034 m. Rechnen wir die Höhe über den Umrechnungsfaktor 3/5 φ2 in die Einheit HE um, erhalten wir exakt 230,2978262 HE (146,6099034 x 3/5 φ2 = 230,2978262). Die Behauptung aus dem Hitat stimmt also durchaus. Irgend jemand muss also im frühen Mittelalter noch gewusst haben, dass Höhe und Grundseite der Cheopspyramide mit der gleichen Maßzahl ausgedrückt werden können! Nur die Maßeinheiten waren in Vergessenheit geraten.
Fazit: Überlieferungen sollten ernst genommen werden, auch wenn sie auf den ersten Blick wenig glaubwürdig erscheinen.
Eine weitere Maßeinheit: Pyramidenzoll (PZ)
Aus Überlieferungen ist bekannt, dass der fünfundzwanzigste Teil einer Heiligen Elle einem Pyramidenzoll entspricht ( 1 HE : 25 = 1 PZ). In Zahlen ausgedrückt: 63,66100186 cm : 25 = 2,546440074 cm. Ich kann mich des Eindrucks nicht erwehren, dass hier jemand dem englischen Zoll (2,54 cm) den Rest abgeschnitten hat.
Die π – Werte im Überblick
Was spricht für die entdeckten π – Werte?
Im 3 1/7 – System läßt sich so der Wert von 440 KE für die Länge einer Grundseite der Cheopspyramide verifizieren und somit die Überlieferung bestätigen.
Das π – antik – System basiert auf eigener Forschung und liefert mit der Grundseitenlänge von 168 GE eine neue Maßeinheit, die dem gesamten Pramidenfeld in Gizeh zu grunde liegt. Über die Heilige Elle (HE) ließ sich sogar die unsinnige Behauptung aus dem Hitat beweisen, dass Grundseitenlänge und Höhe der Cheopspyramide gleich seien.
Im π – phi – System bestätigt sich Herodots Überlieferung, dass die Fläche zweier Oberflächendreiecke gleich ist dem Quadrat der Pyramidenhöhe. Die Berechnung dafür entspringt wieder eigener Forschung. Was ich im Pyramidenfeld von Gizeh aber nicht gefunden habe, ist die Zahl π selbst, die wir standardmäßig zur Kreisberechnung verwenden:
Die fünf Maßeinheiten im Überblick
1m = 5/φ2 KE = 5/φ4 GE = 3/5 φ2 HE = 15 φ2 PZ
| 1m | 100 cm |
| 1KE | 52,3606797 cm |
| 1 HE | 63,66100186 cm |
| 1 PZ | 2,546440074 cm |
| 1 GE | 137,0820394 cm |
Tab.5: Die fünf Maßeinheiten
Die ägyptische königliche Elle eignete sich zusammen mit dem Meter dazu, gerade Zahlen zu generieren. Ist der Radius in der Einheit Meter eine gerade Zahl, so ist der Kreisumfang in der Einheit Meter eine irrationale Zahl (eine Zahl, die kein Ende besitzt). Rechnet man den Umfang aber in die Einheit KE um, so ergibt sich wieder eine gerade Zahl. Beispiel: Kreisradius 2 m; nach der Formel U = 2 x π – antik x r errechnet sich der Umfang zu 12,56656315 m. Nach Multiplikation mit 5/φ2 (Umrechnungsfaktor von der Einheit Meter in die Einheit KE) ergeben sich 24 KE.
Die Heilige Elle (HE) durfte nur für heilige Bauten verendet werden, wahrscheinlich deshalb, weil sie von Erdumfang und Erdradius abgeleitet war und damit die Bauwerke mit dem Planeten Erde in Resonanz standen.
Der Pyramidenzoll (PZ) bringt die Nähe zum englischen Zoll (inch).
Die Grundeinheit (GE) liegt dem ganzen Pyramidenfeld von Gizeh zu grunde. Mit 137,0820394 cm liegt sie numerisch dicht bei der Sommerfeldtschen atomaren Feinstrukturkonstante (137,036).
Was wäre, wenn …
Kehren wir nun zu der eingangs gestellten Frage zurück: Was wäre, wenn mit Hilfe des exakten Wertes für die ägyptische königliche Elle alle vorgenannten Überlieferungen, Vermutungen und Behauptungen sich verifizieren ließen?
Wäre das ein stichhaltiger Beweis für ihre Richtigkeit?
Wäre dies umgekehrt ein stichhaltiger Beweis für die Richtigkeit des gefundenen KE – Werts? Wenn ja, was wären die Konsequenzen für unser heutiges Weltbild?
Der exakte Wert für 1 KE ist gefunden (1/5 φ2). Mit Hilfe dieses Wertes ist bestätigt:
s – Cheops = 440 KE h – Cheops = 280 KE
s – Cheops = 168 GE
h2 – Cheops = 2 x OFD = 78 400 KE2 Herodot
s – Cheops = h – Cheops Hitat
m 230,299 HE
Sind das stichhaltige Beweise? Ich glaube schon. Aber mein Glaube und meine Meinung zählen hier nicht viel. Die hehre Wissenschaft muss prüfen, ob die vorgelegten Tatbestände richtig sind oder nicht.
Sollte die Prüfung den Nachweis der Richtigkeit erbringen, hätte das Konsequenzen für unser bestehendes Weltbild. Denn dann wäre klar, dass die alten Ägypter nicht die Erbauer der Pyramiden in Gizeh um 2500 v.Chr. gewesen sein können. Ihnen stand damals noch nicht das Wissen um Irrationalzahlen und wie man sie zu geraden Zahlen macht zur Verfügung. Auch um Naturkonstanten wie φ wussten sie noch nichts. Insgesamt gesehen handelt es sich hier ja um recht fortgeschrittene Mathematik.
Daraus ergibt sich eine weitere Konsequenz, die in eine Frage mündet: Wenn nicht die Ägypter, wer dann hat die drei Gizehpyramiden erbaut? Und wann? Es müssen Intelligenzen am Werk gewesen sein, die viel mehr wussten als wir heute lebenden Menschen. Unseren Wissenschaftlern heute ist ja noch nicht einmal der Wert von π – phi bekannt, den habe ich erst in den letzten Jahren herausgefunden. Gleichwohl ist er in die Cheopspyramide eincodiert, wie ich in einem der nächsten Kapitel zeigen werde, wenn es um die vier verschiedenen Viertel des Grundquadrats der Cheopspyramide am Boden geht.
In „Der Pyramiden – Code“ wurde dargelegt, dass die Erbauer der drei Gizezh – Pyramiden die Wesen waren, die von den alten Ägyptern als Götter verehrt wurden. Der Zeitraum der Erbauung liegt wahrscheinlich vor der Sintflut, also wahrscheinlich vor 10 500 v.Chr. Es gibt im Hitat diesbezüglich eine Textstelle, wo es heißt, es habe eine Sintflut gegeben, deren Wasser hätten die Spitzen der drei Pyramiden aber nicht erreicht. Sollte das zutreffen, wird der Erbauungszeitraum vor das Sintflutdatum gelegt.
Im Kapitel Der Bauplan der Cheopspyramide werden wir den Fragen nachgehen:
Warum verschiedene π – Werte?
Warum verschiedene Grundseitenlängen?
