Der Bauplan der Cheopspyramide
Daten zur Cheopspyramide
- Höhe (ursprünglich): 146,50 m ca. 280 KE (1 KE = 0,524 m)
- Höhe (heute) etwa 138,75 m
- Neigungswinkel: 51°50´
- Seitenlänge (ursprünglich) geschätzte 230,33 m ca. 440 KE
- Seitenlänge (heute): ca. 225 m
„Eine exakte Bestimmung der ursprünglichen Pyramidenmaße ist jedoch nicht möglich, da Kanten und Flächen heute weitgehend abgetragen und zerstört sind. Dies erschwert beispielsweise eine korrekte Winkelmessung (Neigungswinkel), zudem ist das Bauwerk in seiner Symmetrie selbst nicht perfekt, so dass Abweichungen bei den Vermessungen entstehen. In der ägyptologischen Literatur sind die Angaben nach Peter Janosi, Mark Lehner, Miroslav Verner, Zahi Hawass und Alberto Silotti zum Basismaß der Seitenlänge (230,33 bis 230,37 m) und der aus dem Neigungswinkel berechneten Höhe (146,59 bis 146,60 m) geringfügig abweichend. Die Neigungswinkel werden in neuerer Literatur generell mit 51°50´ angegeben, wobei die Bogensekunden (40´´) meist unberücksichtigt bleiben.“
Obige Zahlenangaben und der Text danach stammen aus: wikivisually/com/lang-de/wiki/Cheopspyramide.
Schauen wir uns die Sache genauer an. Laut der Überlieferung beträgt die Höhe der Cheopspyramide 280 KE. Das entspreche 146,50 m bei der Länge 1 KE von 0,524 m. Rechnet man das nach (280 KE x 0,524 m) erhält man aber 146,72 m. Die Differenz beträgt immerhin 22 cm.
Wie im Das Pyramidenfeld von Gizeh und die ägyptische königliche Elle dargelegt entsprechen 280 KE 146,61 m bei einem Umrechnungsfaktor von 1/5 φ2 m.
Fazit: Literaturangaben kann man nicht blind vertrauen, man sollte alles selbst nachrechnen.
Teilt man 146,50 m durch 280 KE, ergeben sich 0,523214285 m gegenüber behaupteten 0,524 m. Umgekehrt werden in der Literatur keine zehnstelligen Monsterzahlen angegeben, sondern Zahlen, die höchstens bis auf drei Stellen hinter dem Komma genau sind. Um in diesem Beispiel zu bleiben: 280 KE x 0,523 m = 146,44 m. Und schon fehlen sechs Zentimeter. Den restlichen Stellen kommt also durchaus eine Bedeutung zu.
Das Problem besteht darin, dass hier mehrere unterschiedliche Meterwerte für 1 KE zur Berechnung der Pyramidenhöhe benutzt wurden. Dann ist klar, dass auch unterschiedliche Pyramidenhöhen herauskommen. Das zeigt aber die komplette Hilflosigkeit der Ägyptologie, da jeder Autor in Unkenntnis der wahren Länge für 1 KE seinen eigenen Meterwert dafür hat.
Die Lösung kann nur lauten: ein einheitlicher Wert für die ägyptische königliche Elle. Wie im vorangegangenen Kapitel ausgeführt, sollte dieser Wert 1/5 φ2 m sein.
Früher galt die Cheopspyramide als eines der am genauesten ausgeführten Bauwerke der Welt. Angesichts der vielen unterschiedlichen Messwerte – z.B. bei den Seitenlängen – sind heutzutage viele „etwa“, „ca.“ und „geschätzt“ getreten, außerdem sei das Bauwerk in seiner Symmetrie selbst nicht perfekt. Damit wird das vorhandene Unwissen durch „etwa“, „ca.“ und „geschätzt“ ersetzt.
Es nützt alles messtechnische Herumprobieren nichts. Gebraucht wird ein Bauplan, der den Vorort – Daten in Verbindung mit den stattgehabten äußerlichen Veränderungen gerecht wird.
Grundvoraussetzung zur Planung und zum Bau eines Bauwerks sind ein Bauplan und ein Grundmaß, das dem Bauplan zu Grunde liegt. Das Grundmaß ist mit der ägyptischen königlichen Elle zu 1/5 φ2 m vorhanden. Der Bauplan (hier die Außenmaße wie Grundseitenlängen, Seitenhöhen, Polkanten und die Höhe der Pyramide) muss rekonstruiert werden.
Mit dem bekannten Grundmaß kann die Genauigkeit beliebig variiert werden. Zehnstellige Monsterzahlen oder anschauliche gerundete Zahlen stimmen dann immer.
Zwei Arbeitshypothesen
Es gibt angesichts der unterschiedlichen Messergebnisse für die Pyramidenhöhe und für die Längen ihrer Grundseiten (von Autor zu Autor für dieselbe Seite und vom gleichen Autor von Himmelsrichtung zu Himmelsrichtung) zwei mögliche Arbeitshypothesen:
- Alle vier Grundseiten sind gleich lang und die rechten Winkel in den Pyramidenecken betragen alle genau 90°. Die Abweichungen sind entweder Mängel in der Bauausführung oder durch äußere Einflüsse bedingt. Das ist die heute vorherrschende Sichtweise.
- Die Unterschiede sind keine Mängel in der Bauausführung, sondern gewollt und aus bis jetzt noch unerklärten Gründen Teile des Bauplans. Dies ist meine Sichtweise.
Es soll jetzt versucht werden, beide Arbeitshypothesen miteinander zu vergleichen.
Arbeitshypothese 1
Es gab insgesamt drei wichtige Vermessungen der Cheopspyramide.
Die erste wurde von W.M.F. Petrie 1883 durchgeführt und im Buch „The Pyramids and Temples of Gizeh“ 1883 veröffentlicht.
Petrie konstatierte, die Grundseitenlängen dürften nicht von den Eckpfannen aus gemessen werden (Smyth hatte damit vorher Längen um 232,15 m erhalten), sondern vom fast 60 cm höheren Niveau der Pflasterung aus. Damit ergaben sich Längen um 230,30 m. Der Schutt an der Basis lag damals aber noch meterhoch.
J.H.Cole und L.Borchardt führten 1925 gemeinsam eine weitere Vermessung durch. Der Schutt war teilweise abgetragen, es waren an den Messstellen aber Grabungen von bis zu vier Meter bis auf die Pflasterung nötig. Cole veröffentlichte seine Ergebnisse 1925 im Buch „Determination of the Exact Site and Orientation of the Great Pyramid of Giza“. Borchard präsentierte seine Resultate 1926 im Buch „Längen und Richtungen der vier Grundkanten der großen Pyramide bei Gise“.
Als nächstes vermaß W.Dorner 1979 die Cheopspyramide. Jetzt war der Schutt vollständig abgetragen. Benutzt wurden im Wesentlichen dieselben Messlinien wie 1925. Dorners Ergebnisse erschienen 1981 in „Absteckung und Orientierung ägyptischer Pyramiden“.
Unter der Leitung des amerikanischen Ägyptologen Mark Lehner erfolgte ab den 1984er Jahren eine weitere satellitengestützte Vermessung des gesamten Gizeh – Plateaus, das sogenannte GPMP (Gizeh Plateau Mapping Project). Leider stehen die dabei erzielten Messergebnisse der Öffentlichkeit immer noch nicht zur Verfügung. Es existieren sogenannte Gitternetzkarten wie z.B. im 2018 erschienenen Buch von A.Collins „Der Schwan“. Daraus lassen sich aber für keine der drei Pyramiden verlässliche Grundseitenlängen ableiten.
Als Gitternetz wurden Quadrate mit einer Seitenlänge von 100 m verwendet. Es handelt sich um ein Quadrat von 1300 x 1300 m. Die Nordwestecke der Cheopspyramide befindet sich im Plan bei genau 600 m Ost – West – Richtung und 100 m Nord – Süd – Richtung. Die Südwestecke der Mykerinospyramide liegt bei 1000 m in Nord – Süd – Richtung und bei 100 m in Ost – West – Richtung. Damit ist die lange Seite des Rechtecks ziemlich genau 900 m lang und die kurze Seite ziemlich genau 730 m.
Vergleicht man das mit meinem Plan des Gizeh – Plateaus aus dem vorigen Kapitel, zeigt sich, dass 672 GE 921,19 m sind und 560 GE 767,66 m. Für die lange Seite ergibt sich eine Differenz von 21,19 m und für die kurze Seite von 37,66 m.
Erstaunlich finde ich es allerdings, dass sowohl eine Pyramidenecke der Cheops- – als auch eine der Pyramidenecken der Mykerinospyramide genau auf Gitternetzpunkten liegen. Bei meiner ganzen Recherche habe ich keinen einzigen ganzzahligen Meterwert gefunden. Ganze Zahlen traten nur bei den Einheiten GE, KE, HE und PZ auf.
Da bis jetzt keine verbindlichen Koordinaten veröffentlicht sind, muss das erst mal so stehen bleiben, wie ich es hier beschrieben habe. Für mich sind die Differenzen zu meinem Plan recht groß. Aber Genaueres zum GPMP lässt sich mangels verfügbarer belastbarer Daten nicht sagen.
Kehren wir nun zu den Vermessungen der Cheopspyramide zurück.
| Nordseite [m] | Südseite [m] | Ostseite [m] | Westseite [m] | |
| Petrie 1883 | 230,363 | 230,365 | 230,3196 | 230,342 |
| Cole 1925 | 230,253 | 230,454 | 230,391 | 230,357 |
| Dorner 1979 | 230,328 | 230,372 | 230,369 | 230,372 |
Tab.1: Die Grundseitenlängen der Cheopspyramide
Tabelle 1 zeigt die Messresultate der drei zitierten Vermessungen. Es existieren Unterschiede bis zu 20 cm. Das ist zu groß, um daraus einen verlässlichen Bauplan abzuleiten.
Bei allen drei Vermessungen wurde auch der Azimut jeder Grundseite gemessen. Der Azimut ist die Abweichung einer Linie von der genauen Nordrichtung und wird im Uhrzeigersinn gemessen (siehe Abb.1).
| Nordseite [°] | Südseite [°] | Ostseite [°] | Westseite [°] | |
| Petrie 1883 | 89°56´40´´ | 89°56´03´´ | 359°56´19´´ | 359°56´06´´ |
| Cole 1925 | 89°57´32´´ | 89°58´03´´ | 359°54´30´´ | 359°57´30´´ |
| Dorner 1979 | 89°57´32´´ | 89°57´29´´ | 359°56´34´´ | 359°57´13´´ |
Tab.2: Azimuttabele 1
Tabelle 2 zeigt die gemessenen Werte, Tabelle 3 die Abweichungen zum rechten Winkel. Alle Messwerte liegen bei weniger als 90° und weniger als 360°. Der Azimut bezeichnet also die Genauigkeit der rechten Winkel in den Pyramidenecken.
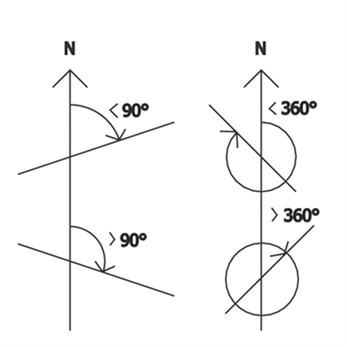
Abb.1: Der Azimut
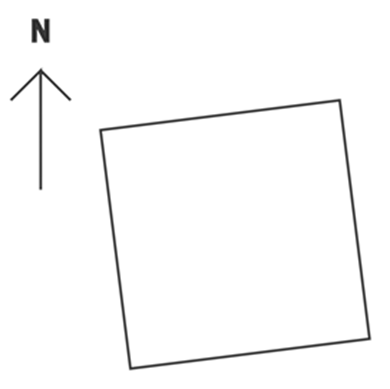
Abb.2: Ausrichtung Cheopspyramide
| Nordseite [°] | Südseite [°] | Ostseite [°] | Westseite [°] | |
| Petrie 1883 | – 3´20´´ | -3´57´´ | -3´41´´ | -3´54´´ |
| Cole 1925 | – 2´28´´ | -1´57´´ | -5´30´´ | -2´30´´ |
| Dorner 1979 | – 2´28´´ | -2´31´´ | -3´26´´ | -2´47´´ |
Tab.3: Azimuttabelle 2
Abbildung 2 zeigt in stark übertriebener Form die Ausrichtung der Grundfläche der Cheopspyramide in Bezug zur genauen Nordrichtung.
In ähnlicher Form schauen wir uns nun die drei Vermessungen im Einzelnen an.
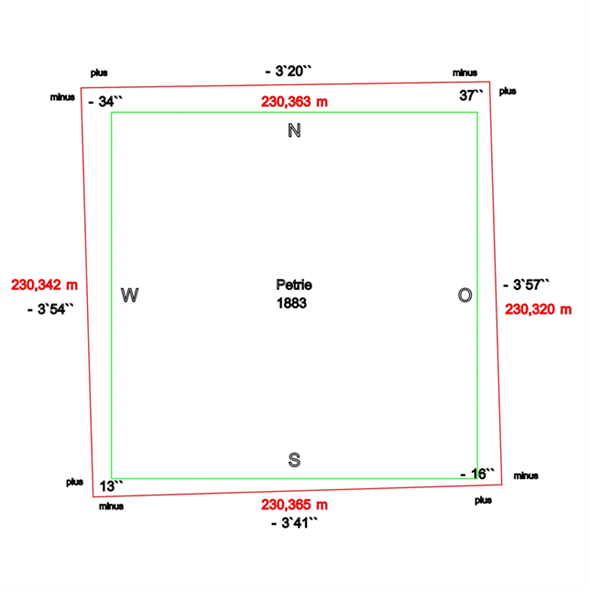
Abb.3: Petrie 1883
Petrie (siehe Abb.3) hat Seitenlängen zwischen 230,32 m und 230,365 m gemessen. Die Differenz von kleinster und größter Seitenlänge beträgt gerade einmal 4,5 cm. Die Azimute liegen zwischen 3 und 4 Winkelminuten, die Abweichung vom rechten Winkel in den Pyramidenecken befinden sich im niedrigen Sekundenbereich.
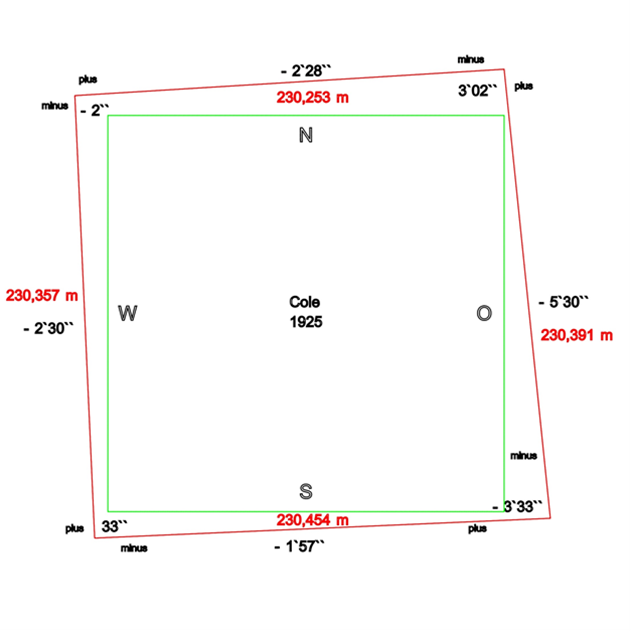
Abb.4: Cole 1925
Bei Coles Vermessung 1925 (siehe Abb.4) sind die Unterschiede größer. Hier finden sich Grundseitenlängen zwischen 230,253 m und 230,454 m. Die Differenz beträgt 20,1 cm. Auffällig ist die große Länge der Südseite. Die Azimute liegen um zwei Winkelminuten, die Ostseite hat allerdings den Wert 5´30´´. Die Abweichungen vom rechten Winkel in den Pyramidenecken reichen von 2´´ bis 3´33´´.
Cole ging so vor: Dort, wo noch Verkleidungsblöcke vorhanden waren, suchte er den Außenrand der Unterseite des Verkleidungsblocks auf. Mittels Theodolith maß er die Länge zwischen zwei Markierungen innerhalb der Ausschachtung. Ebenfalls mittels Theodolith verlängerte er diese Linie bis zu den Pyramidenecken und legte die Schnittpunkte der Linien in den Pyramidenecken fest. Dieser Vorgang wurde zwei bis drei mal wiederholt. Es wurden Unterschiede bis zu 3 cm gemessen. Der Durchschnitt aller Markierungen wurde als bestmögliches Ergebnis erachtet. Gemessen wurde mit einem Stahlband, das in Zentimeter geeicht war, Millimeter wurden geschätzt.
Abb.5 zeigt Einzelheiten der Vermessung. Auf der Nordseite war keine Grabung erforderlich, die Linie war auf 55 m auffindbar, davon 20 m Verkleidung. Auf der Ostseite erfolgte von der Seitenmitte 29 m nach Norden eine Grabung, die aufzufindende Linie war fast auf der gesamten Grabungslänge da. Auf der Südseite waren fünf Grabungen erforderlich. In einer Grube fand sich die Oberkante von Verkleidungsblöcken auf 26 m Länge. Auf der Westseite gab es vier Grabungen, in drei Fällen ließ sich die Linie auffinden auf insgesamt 37 m Länge.
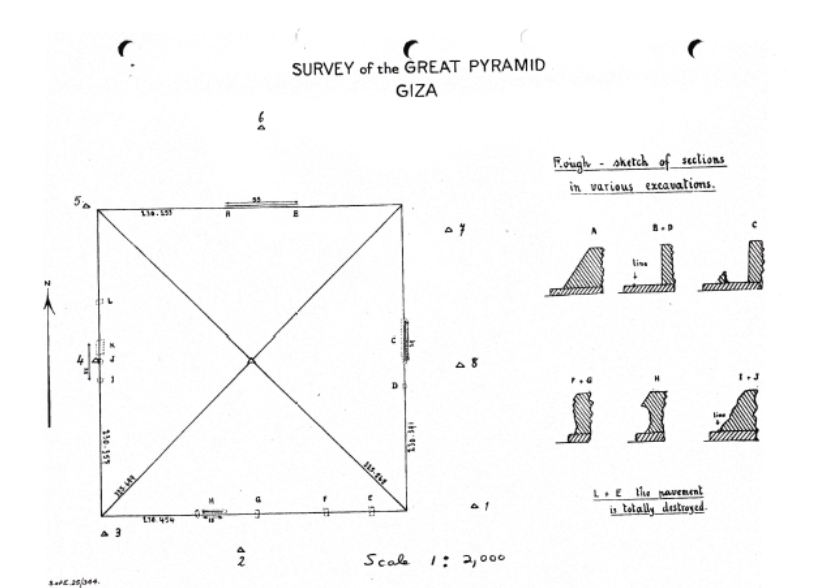
Abb.5: Coles Vermessungsprotokoll
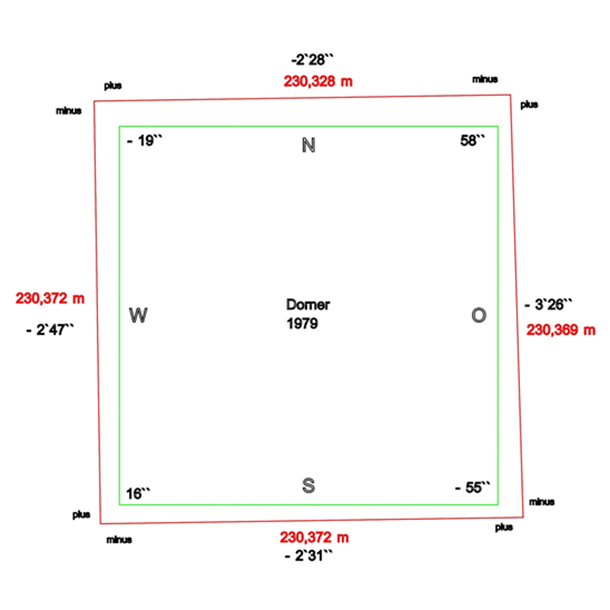
Abb.6: Dorner 1979
Dorner maß 1979 (siehe Abb.6) Seitenlängen zwischen 230,328 m und 230,372 m. Die Differenz beträgt ähnlich wie bei Petrie 4,4 cm. Die Azimute liegen zwischen 2´30´´ und 3´30´´. Die Abweichungen vom rechten Winkel in den Pyramidenecken befinden sich im niedrigen und hohen Sekundenbereich.
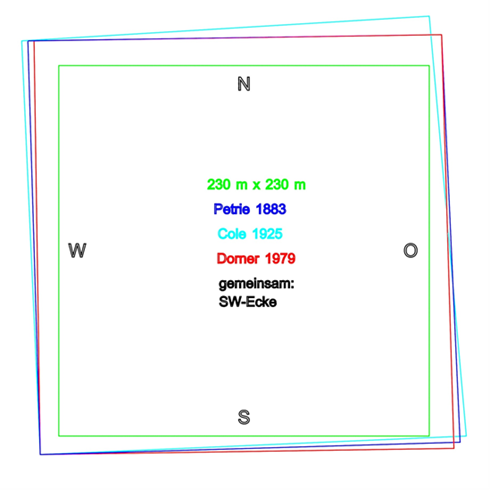
Abb.7: Alle drei Vermessungen auf eine gemeinsame Südwestecke projiziert
Abb.7 zeigt die Projektion der drei Vermessungen auf eine gemeinsame Südwestecke. Die Messresultate von Petrie und Dorner sind vergleichbar und ähneln einander. Cole scheint Schwierigkeiten mit dem Auffinden der Messlinie auf der Südseite gehabt zu haben, sein Messergebnis dafür ist 8,9 cm länger als das von Petrie und 8,2 cm länger als das von Dorner.
Wir wollen jetzt an Hand der Ergebnisse von Cole versuchen, die Abweichung vom rechten Winkel in den Pyramidenecken zu bewerten (siehe Tab.4).
| NW – Ecke | 2´´ | 0,00056° |
| NO – Ecke | 3´ 2´´ | 0,05056° |
| SO – Ecke | 3´33´´ | 0,059167° |
| SW – Ecke | 33´´ | 0,009167° |
Tab.4: Abweichung vom rechten Winkel in den Pyramidenecken (Cole 1925)
Das schlechteste Ergebnis ist in Bogengrad ausgedrückt etwas mehr als 5/100°. Das ist immer noch eine atemberaubende Präzision in der Bauausführung.
Ein Kreis besteht aus 360° (Bogengrad) oder 21 600´ (Bogenminuten) oder 1 296 000´´ (Bogensekunden). Unterteilt man einen Kreis nun in seine fast 1,3 Millionen Bogensekunden, bedeutet eine Abweichung von 2´´ (bestes Ergebnis) zwei Teile dieses Kreises, eine Abweichung von 3´33´´ (schlechtestes Ergebnis) 213 Teile.
Der Unterschied der Seitenlängen liegt zwischen 3 cm und 20 cm. Um einen Unterschied von 1 m zu bekommen müsste die Abweichung vom rechten Winkel in einer Pyramidenecke schon etwa ¼° betragen, das wären dann etwa 900 dieser Kreisteile.
An hand der Messwerte von Cole 1925 will ich dies noch etwas anschaulicher gestalten. Die Ostseite (230,391 m) ist um 3,4 cm länger als die Westseite (230,357 m). Die Südseite ist 230,454 m lang.
Wendet man darauf den Satz des Pthagoras an (230,4542 + 0,0342 = 230,45400252), ergibt das eine Verlängerung der Südseite um 25/10 000 mm (siehe Abb.8). Das können wir noch nicht einmal vernünftig messen.
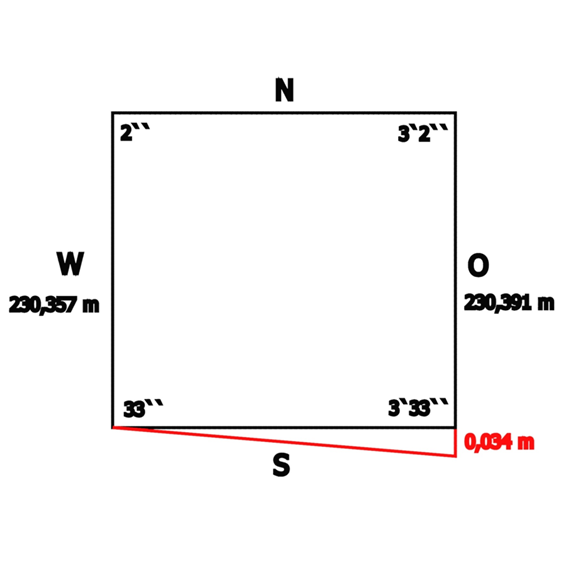
Abb.8: Verlängerung der Südseite
Angesichts dieser doch winzigen Unterschiede auf einer Länge von mehr als 230 m kann die Arbeitshypothese, dass alle vier Grundseiten gleich lang und die Winkel in den Pyramidenecken genau 90° sind und dass es sich bei den Unterschieden um Mängel in der Bauausführung oder äußere Einflüsse handelt, nicht widerlegt werden.
Arbeitshypothese 2
Die Cheopspyramide bietet aber noch mehr als Grundseitenlängen und rechte Winkel in den Pyramidenecken.
Wir wollen nun Arbeitshypothese zwei beleuchten. Diese führt zur folgenden Annahme: Die vier Grundseiten der Cheopspyramide sind tatsächlich verschieden lang. Warum?
Meine Forschung hat ergeben, dass die Grundfläche der Cheopspyramide in vier unterschiedliche Viertel aufgeteilt ist (siehe Abb.9). Hier kommen die drei π – Werte aus Kapitel 1 ins Spiel.
Jedem Viertel der Grundfläche liegt ein anderer π – Wert zu Grunde. Nach der Formel 1/4 π – Wert x h lässt sich die halbe Grundseitenlänge berechnen. Im Unterschied zur Ägyptologie hat jetzt jede Pyramidenseite zwei unterschiedlich lange Halbseiten. In der Mitte jeder Seite gibt es sogenannte Rücksprünge, die bautechnisch für den Ausgleich sorgen. In Abb.9 ist das stark übertrieben dargestellt.
Im von π – phi repräsentierten Viertel findet sich Herodots Überlieferung, dass das Quadrat der Höhe flächengleich mit zwei der Oberflächendreiecke sei. Die Oberflächendreiecke befinden sich auf dem rechten Teil der Südseite und dem unteren Teil der Ostseite. Sie sind über die Polkante der Südostecke, die zur Pyramidenspitze läuft, miteinander verbunden.
Drei der vier π – Werte kennen wir schon: π – antik, 3 1/7 und π – phi.
Im 2002 erschienenen Buch „Der Pyramiden – Code“ habe ich als vierten π – Wert 3,14 angegeben. Im Zuge der weiteren Forschung hat sich aber ergeben, dass an dieser Stelle der Wert π – phi – Partner stehen muss. Was ist ein π – Partner?
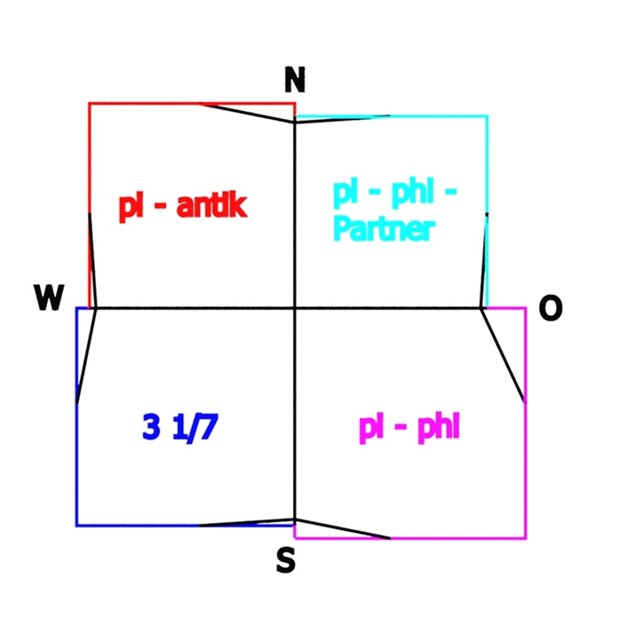
Abb 9: Die verschiedenen Viertel der Pyramidengrundfläche
π – Partner
π beschränkt sich nicht auf die Zahl π, sondern ist ein Bereich. Schon Archimedes sagte: „Das Verhältnis des Umfangs eines beliebigen Kreises zu seinem Durchmesser ist kleiner als 3 1/7, aber größer als 3 10/71“ (siehe Tab.5).
| 3 10/71 | < | π | < | 3 1/7 |
| 3,14084507 | 3,141592654 | 3,142857143 |
Tab.5: Der π – Bereich
Was Archimedes nicht wusste (unsere heutigen Mathematiker aber auch nicht!): Innerhalb dieses Bereichs gibt es Produktpartnerschaften in Form von je zwei Zahlenwerten, die zu einer einzigen Zahl (= Produktkonstanten) hinführen.
πD2 = 9,873728189 = 3,1422489062 = πD x πD
πD bezeichne ich als das Dorchschnitts – π. Die mathematische Herleitung folgt im nächsten Kapitel. Wenn man die π – Partner miteinander multipliziert, erhält man immer die Zahl 9,873728189, eine neue wissenschaftliche Konstante.
3 1/7 und π – antik sind solche π – Partner. So liegt es nahe, für das vierte Pyramidenviertel den Partner von π – phi zu verwenden (siehe Tab.6)
| 3 1/7 x πantik | = | πD2 | = | πphi x πphi-Partner |
| 22/7 x 6/5 φ2 | = | 132/35 φ2 | = | 4/φ0,5 x 33/35 φ2,5 |
| 3,143 x 3,1416 | = | 9,874 | = | 3,1446 x 3,140 |
Tab.6: π – Partner
Drei der vier π – Werte stehen über die Zahl φ in Verbindung. Die Pyramidenviertel an der Basis garantieren die rechten Winkel in den Pyramidenecken. Die Rücksprünge der Grundseiten sorgen bautechnisch für den Ausgleich.
Die Rücksprünge in den Seiten der Cheopspyramide
Die Rücksprünge gibt es auf allen vier Seiten.

- Bild: P.Lemesurier Geheimcode Cheops
- Bild 1: Cheopspyramide mit Rücksprung
Wegen der verschiedenen π – Werte sind die vier Grundseiten alle verschieden lang. Die Pyramide ist so genial konstruiert, dass für alle vier Pyramidenviertel immer dasselbe Höhenniveau resultiert, so dass sich die vier Polkanten in der Spitze treffen.
Die Pyramidenhöhe ist eine Produktkonstante. Das hängt mit dem Tangenswert zusammen. Der Tangens eines Winkels ist das Verhältnis von Gegenkathete zu Ankathete. Für den Neigungswinkel an der Pyramidenbasis in Seitenmitte heißt das, der Tangens ist das Verhältnis von Pyramidenhöhe zur halben Seitenlänge.
tan α = Gegenkathete : Ankathete = h : ½ s
Löst man das nach h auf, ergibt sich:
h = ½ s x tan α.
Wenn ½ s etwas größer wird, wird tan α etwas kleiner, so dass die Höhe h immer gleich bleibt. Mit diesem Kniff war garantiert, dass beim Bau trotz vier verschiedener Neigungswinkel an der Pyramidenbasis in allen vier Pyramidenvierteln immer dasselbe Höhenniveau herrschte.
Peter Lemesurier schreibt in Geheimcode Cheops:
„An jeder Pyramidenseite hat der Architekt einen deltaförmigen Mauerrücksprung geschaffen, der genau dem Querschnitt der Pyramide zu einem fünftel ihrer Realgröße entspricht.“

- Bild: H. Rauprich Cheops
- Bild 2: Flachdreieck Südseite
Wie passen die Rücksprünge zu den geraden Seitenlinien? Sowohl Cole als auch Borchardt betonen ausdrücklich, dass die Messungen am Boden gerade Linien sind. Lösung: Die Außenkanten der Unterseiten der untersten Lage der Verkleidungsblöcke, wo Cole und Borchardt ihre Messungen durchgeführt haben, ergeben gerade Linien. Deren Vorderfläche zur Oberkante hin (die sichtbare Verkleidung) muss so gearbeitet sein, dass die Rücksprünge entstehen. Ab der zweiten Schicht der Verkleidungsblöcke müssen deren Außenkanten keine geraden Linien mehr ergeben.
Die Rücksprünge sollen in Seitenmitte über 90 cm tief sein.
Peter Lemesurier schreibt, dass die Rücksprünge bis zu einem fünftel der Realgröße der Pyramide reichen. Damit ist die Höhe gemeint. Schaut man sich aber Bild 2 an, wird ersichtlich, dass das sichtbare Flachdreieck etwa dem Siebtel der Pyramidenhöhe entspricht, das sind 40 KE. Horizontal beginnt es etwa nach 2/7 der Seitenlänge, erstreckt sich über 3/7 der Seite und endet nach 5/7. Setzt man die Seitenlänge zu 168 GE an, beginnt das Flachdreieck nach 48 GE, ist 72 GE lang und endet nach 120 GE. 36 GE sind ungefähr 50 m. Bei einer Rücksprungtiefe in Seitenmitte von etwa 1 m sind das horizontal 2 cm pro Meter Verkleidung. Das sollte bautechnisch machbar sein und würde optisch kaum erkennbar sein.
Warum von unterschiedlichen π – Werten repräsentierte vier verschiedene Viertel für die Cheopspyramide?
Die in Kapitel 1 dargestellte Vermutung, der Umfang der Cheopspyramide geteilt durch ihre doppelte Höhe ergebe π, hat zur geraden Seitenlänge von 440 KE geführt und damit zum π – Wert von 3 1/7.
Der Wert der Königselle geteilt durch φ2 führte zur Grundeinheit (GE) und zur geraden Seitenlänge 168 GE und damit zum π – Wert πantik.
Herodots Überlieferung, das Quadrat über der Höhe sei flächengleich mit zwei Oberflächendreiecken, führte zum geradzahligen Flächeninhalt von 78 400 KE2 und damit zum dritten π – Wert πphi.
Für das vom π – Partner von πphi repräsentierte vierte Pyramidenviertel habe ich keine derartigen Umstände gefunden, hier sollte die π – Partnerschaft als Grund ausreichen.
Der Untergrund der Cheopspyramide
Cole schreibt, dass auf soliden Fels eine sorgfältig nivellierte Pflasterung aufgebracht wurde. Auf dieser Pflasterung wurden die Kalksteinblöcke an der Pyramidenbasis verlegt. Die Strecke vom Außenrand der untersten Verkleidungsblöcke bis zum Außenrand der Pflasterung betrug etwa 40 cm.
Cole gibt für die Nordseite 42 cm an, für die Ostseite 48 cm und für die Westseite 38 cm. Für die Südseite erfolgte keine Angabe. Cole schreibt leider nicht, wo genau die Abstandsmessungen erfolgten, er spricht nur von Orten, an denen eine Messung möglich war.
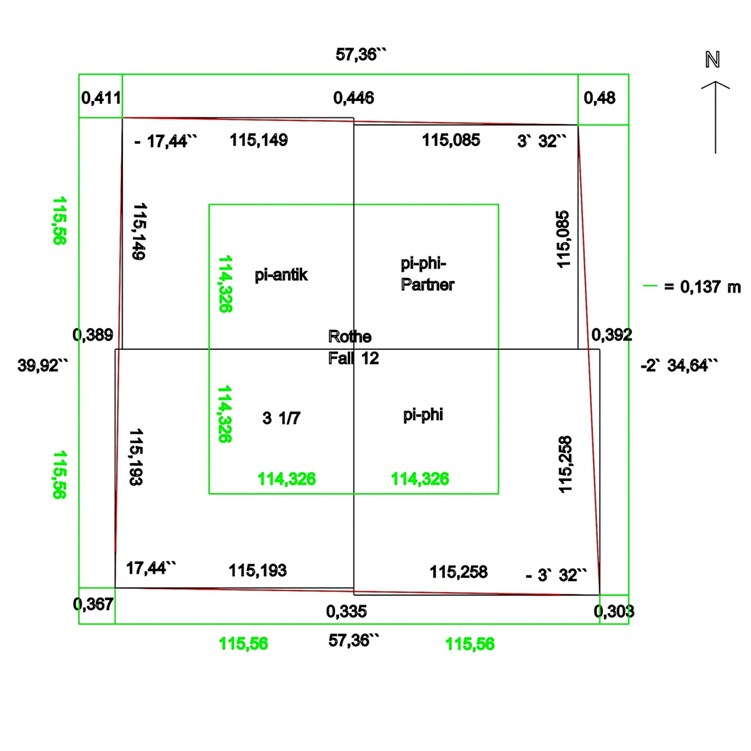
- Abb. 10: Vergleich Rothe Fall 12 mit Cole
- Äußere grüne Linie bei 84,3 GE = Außenrand Pflasterung
- Innere grüne Linie bei 83,4 GE = Grenze der Rücksprünge in
- den Seitenmitten
- Rote Linie: Verlauf der vier Grundseiten
Es gibt insgesamt 24 Möglichkeiten, die vier π – Werte als Pyramidenviertel miteinander zu kombinieren. Dabei ist zu beachten, dass die zur Grundseitenlänge kombinierten zwei Halbseitenlängen nicht größer, höchstens gleich den gemessenen Werten sind. Durch den großen Druck des steinernen Bauwerks von oben und eventuell auch durch die gewaltige Sonneneinstrahlung tagsüber können diese äußeren Einflüsse im Sinne einer Vergrößerung Auswirkungen auf die Seitenlängen der Pyramide haben.
Aber welche Messwerte soll man zum Vergleich heranziehen? Petries und Dorners Vermessungen ähneln einander sehr, da sie nur geringe Abweichungen der vier verschiedenen Grundseitenlängen zeigen.
Coles und Borchardts Werte differieren dagegen stärker und sollen deshalb als Vergleichsgrundlage dienen.
Rothe Fall 12 bietet die meisten Übereinstimmungen mit den Vermessungsdaten von Cole (siehe Tabellen 7 und 8).
| Cole 1925 | Seitenlänge | Azimut | |
| N | 230,253 m | 89° 57` 32„ | – 2` 28„ |
| O | 230,391 m | 359° 54` 30„ | – 5` 30„ |
| S | 230,454 m | 89° 58` 03„ | – 1` 57„ |
| W | 230,357 m | 359° 57` 30„ | – 2` 30„ |
| NW – SO | 325,868 m | 314° 57` 03„ | – 2` 57„ |
| NO – SW | 325,699 m | 44° 56` 45„ | – 3` 15„ |
Tab.7: Coles Messwerte 1925
| Rothe Fall 12 | Seitenlänge | Azimut | |
| N | 230,234 m – 1,9 cm | 90° 00` 57,36„ | 57,36„ |
| O | 230,343 m – 4,8 cm | 359° 57` 25,36„ | – 2` 34,64„ |
| S | 230,451 m – 0,3 cm | 90° 00` 57,36„ | 57,36„ |
| W | 230,342 m – 1,5 cm | 360° 00` 39,92„ | 39,92„ |
| NW – SO | 325,844 m – 2,4 cm | 315° | 0,00„ |
| NO – SW | 325,663 m – 3,6 cm | 45° | 0,00„ |
Tab. 8: Rothe Fall 12
Die Seitenlängen und die Diagonalen sind im Bauplan (Rothe Fall 12) alle etwas kleiner als die Werte von Cole, so dass noch Raum bleibt für die oben besprochenen äußeren Einflüsse. Die Azimute stimmen aber nicht.
Verändert man die Azimute aller vier Grundseiten um – 3`, stimmen sie mit den Cole – Werten sehr gut überein (siehe Tab. 9 und 10). 1301 n.Chr. ereignete sich ein Erdbeben, bei denen die Gizeh – Pyramiden fast ihre komplette Verkleidung verloren. Könnte das zu einer Rotation von – 3` und zu einer leichten Verformung geführt haben?
Dazu müsste man eine Kraft postulieren, die auf die Gesamtkonstruktion (Pflasterung + Pyramide) einwirkte und zu einer Rotation um – 3` und einer Verlängerung der Ostseite um etwa 4 cm führte. Durch die Verlängerung der Ostseite wird die Nordseite um 0,036 mm länger.
Die verbleibenden geringen Differenzen der Seitenlängen von Fall 12 zu Cole (N – 1,9 cm, O – 0,8 cm, S – 0,3 cm, W – 1,5 cm) können durch den natürlichen Druck des Gewichts der Steine von oben entstanden sein.
Damit wäre eine Übereinstimmung des originären Bauplans mit der heute vorgefundenen Situation hergestellt.
| Vergleich der Azimute ▲ Rotation | ||||
| Cole | Fall 12 | Fall 12 – 3` | Differenz | |
| N | – 2`28´´ | + 57,36„ | – 2`02,64„ | + 25,36„ |
| O | – 5`30„ | – 2`34,64„ | – 5`34,64„ | – 4,64„ |
| S | – 1`57„ | + 57,36„ | – 2`02,64„ | – 5.64„ |
| W | – 2`30„ | + 39,92„ | – 2`20,08„ | + 9,92„ |
Tab. 9: Vergleich Rothe – Cole Rotation und Azimute
| Vergleich der Winkel in den Pyramidenecken ► Verformung | |||
| Cole | Fall 12 | Differenz zu Cole | |
| NW | – 02„ | – 17,44„ | – 15,44„ |
| NO | + 3` 02„ | + 3` 32„ | – 30,00„ |
| SO | – 3` 33„ | – 3` 32„ | + 1,00„ |
| SW | + 33„ | + 17,44„ | + 15,56„ |
Tab. 10: Vergleich Rothe – Cole Verformung
Abschließend gebe ich noch eine Tabelle der 24 möglichen Kombinationen der vier verschiedenen Pyramidenviertel unter fünf unterschiedlichen Prämissen:
- Seitenlänge </= Cole
- Diagonale </= Cole
- Azimut +/- 1` zu Cole nach Rotation um – 3`
- Gemessener Abstand zur Pflasterung innerhalb Bauplan
- Borchardt – Linie +/- 5 cm
Rothe Fall 12 erfüllt die Kriterien a bis d, nur das fünfte Kriterium, die Borchardt Linie wird nicht erfüllt.
Die Borchardt – Linie
Prof. Borchardt, der 1925 die Vermessung mit Cole zusammen durchgeführt hat, schreibt: „Dann fand sich (auf der Nordseite, a.d.A.) unter dem östlichsten Verkleidungsblock hervorstehend ein kurzes Stück einer nach Norden gerichteten Linie eingekratzt, das sicher nicht das vielleicht zu lang geratene Ende einer Fugenmarke war. Ich sprach es sogleich als das Nordende der auf dem Pflaster aufgezeichneten Nord – Süd – Achse der Pyramide an.“
Diese Linie konnte ich bei keinem meiner Ägyptenbesuche auffinden, wahrscheinlich existiert sie heute nicht mehr.
Der genaue Abstand der Linie beträgt:
- Zur NW – Ecke 115,090 m
- Zur NO – Ecke 115,161 m
Die halbe Seitenlänge Rothe Fall 12 beträgt
- NW – Viertel 115,149 m πantik
- NO – Viertel 115,085 m πphi – Partner
Es würde fast genau passen, wenn πantik und πphi – Partner die Plätze tauschen würden. Das wäre Rothe Fall 1.
| a N | a O | a S | a W | b NW-SO | b NO-SW | c N | c O | c S | c W | d N | d O | d S | d W | e W/O | |
| 1 | ja | ja | ja | ja | ja | nein | nein | nein | nein | nein | ja | nein | ja | ja | +/+ |
| 2 | ja | nein | ja | ja | ja | nein | nein | ja | ja | nein | ja | nein | ja | ja | +/+ |
| 3 | nein | nein | ja | ja | ja | nein | nein | nein | ja | ja | ja | nein | nein | nein | +/- |
| 4 | nein | nein | ja | ja | ja | nein | nein | nein | nein | nein | ja | nein | nein | ja | +/- |
| 5 | nein | nein | ja | ja | ja | nein | nein | nein | ja | ja | ja | nein | ja | nein | +/+ |
| 6 | nein | ja | ja | ja | ja | nein | nein | nein | nein | nein | ja | nein | ja | ja | +/+ |
| 7 | nein | ja | ja | ja | ja | nein | nein | nein | nein | ja | nein | ja | nein | ja | -/- |
| 8 | nein | nein | ja | ja | ja | nein | nein | nein | ja | nein | nein | nein | nein | nein | -/- |
| 9 | nein | nein | ja | ja | ja | ja | nein | nein | nein | nein | nein | nein | ja | nein | -/+ |
| 10 | nein | ja | ja | nein | ja | nein | nein | nein | nein | nein | nein | nein | ja | ja | -/+ |
| 11 | ja | ja | ja | nein | ja | nein | ja | ja | nein | nein | ja | ja | ja | ja | -/- |
| 12 | ja | ja | ja | ja | ja | ja | ja | ja | ja | ja | ja | ja | ja | ja | -/- |
| 13 | nein | ja | ja | ja | ja | ja | ja | nein | ja | nein | nein | nein | nein | ja | -/+ |
| 14 | nein | ja | ja | nein | ja | nein | ja | nein | nein | nein | nein | ja | nein | ja | -/+ |
| 15 | nein | ja | ja | nein | nein | ja | nein | ja | ja | nein | ja | ja | nein | ja | -/- |
| 16 | nein | ja | ja | nein | ja | ja | nein | nein | nein | nein | ja | ja | nein | nein | -/- |
| 17 | nein | ja | ja | nein | ja | nein | nein | nein | nein | nein | nein | ja | nein | nein | -/+ |
| 18 | nein | ja | ja | ja | nein | ja | nein | nein | ja | nein | nein | nein | nein | ja | -/+ |
| 19 | nein | ja | ja | ja | nein | ja | nein | ja | ja | nein | ja | ja | ja | ja | -/- |
| 20 | nein | ja | ja | nein | ja | nein | nein | nein | nein | ja | ja | ja | ja | nein | -/- |
| 21 | nein | ja | ja | nein | ja | nein | ja | nein | nein | ja | nein | ja | ja | nein | -/+ |
| 22 | nein | nein | ja | ja | nein | ja | ja | ja | nein | nein | nein | nein | ja | ja | -/+ |
| 23 | nein | ja | ja | ja | ja | nein | nein | nein | nein | nein | nen | ja | nein | ja | -/- |
| 24 | nein | nein | ja | ja | ja | nein | nein | nein | ja | nein | nein | nein | nein | ja | -/- |
Tab.11: Die 24 Fälle (Rothe 1 – Rothe 24)
Wie aus Tabelle 11 zu entnehmen ist, wären neun Tatbestände erfüllt und sechs nicht erfüllt, wohingegen bei Fall 12 nur das Kriterium der Borchardt – Linie nicht erfüllt ist.
Die zwei Arbeitshypothesen
Was spricht für Arbeitshypothese 1? Sie ist nicht zu widerlegen.
Was spricht für Arbeitshypothese 2? Sie erklärt die verschieden langen Grundseiten der Pyramide, was zu den vier verschiedenen Pyramidenvierteln führt und die Rücksprünge in den Seitenmitten zu einer bautechnischen Notwendigkeit werden läßt. Sie erklärt auch die besprochenen Überlieferungen und Vermutungen.
Im Internet tauchte im Juni 2022 eine mehrseitige Arbeit auf (Franck Monnier „The so – called concave faces of the Great Pyramid.Facts and cognitive bias“ bei Research Gate, Project Ancient Egyptian Architecture), die die Rücksprünge dadurch erklärt, dass früher Araber und Touristen die Pyramide vorwiegend in den Seitenmitten bestiegen und vermehrt Steinblöcke herausgelöst hätten, die dann mit großem Getöse die Wände herabgefallen seien und auf diesem Weg viele andere Steinblöcke beschädigt hätten. Der Autor konnte keinen vernünftigen anderen Grund für die Existenz der Rücksprünge finden und kam wohl so zu dieser für mich etwas abenteuerlichen Schlussfolgerung.
In meiner Sicht sind die Rücksprünge bei vier unterschiedlichen Pyramidenvierteln eine bautechnische Notwendigkeit.
Arbeitshypothese 2 bietet auch Erklärungen an für die unterschiedlichen Azimute, den Abstand zur Pflasterung, die Rücksprünge und Flachdreiecke. Somit halte ich es für überaus wahrscheinlich, dass die vier Grundseiten der Cheopspyramide tatsächlich unterschiedlich lang sind und dass dies Teil des Bauplans war.
Was spricht gegen Arbeitshypothese 1? Arbeitshypothese 2.
Was spricht gegen Arbeitshypothese 2? Es sind Rotations – und Verformungskräfte als Postulate erforderlich. Trotzdem kann keiner der 24 möglichen Fälle alle aufgestellten Kriterien erfüllen. Lediglich die Vermessungen von Cole und Borchardt werden erklärbar, die von Petrie 1883 und Dorner 1979 aber nicht. Hier ist bei den Rothe – Fällen im Vergleich zu den Messungen von Petrie und Dorner die Südseite zu groß.
Ich neige klar zu Arbeitshypothese 2, weil sie vieles, wenn auch nicht alles erklärt. Zur Frage der Rotations – und Verformungskräfte müssten Geologen gehört werden, danach könnte dann eine Neubewertung erfolgen.
Mit den fünf verschiedenen Maßeinheiten und dem Konzept der vier verschiedenen Pyramidenviertel haben wir ein Arsenal für die Rekonstruktion des Bauplans der Pyramide zur Hand, das wir nutzen sollten. Auch die anderen 22 möglichen Fälle sollten wir nicht gänzlich aus den Augen verlieren, auch wenn dann andere Rotations – und Verformungskräfte postuliert werden müssten.
