Variationen in π
Die Cheopspyramide und π
Jedes Pyramidenviertel steht für ein eigenständiges π (siehe „Der Bauplan der Cheopspyramide“, Abb.9)
| Pyramidenviertel | |||||
| NW | πantik | = | 6/5 φ2 | = | 3,141640787 |
| SW | 3 1/7 | = | 22/7 | = | 3,142857143 |
| SO | πphi | = | 4/φ0,5 | = | 3,144605511 |
| NO | πphi – Partner | = | 33/35 φ2,5 | = | 3,139894068 |
Tab.1: Die verschiedenen π – Werte
Multipliziert man die π – Partner πantik und 3 1/7 miteinander, erhält man die Produktkonstante 132/35 φ2 = 9,873728186 = πD2. πD ergibt sich dann zu 3,142248906. πD2 ergibt auch die Multiplikation von φphi und πphi – Partner. Das Durchschnittspi und sein Quadrat sind zwei neue, der Wissenschaft noch nicht bekannte Zahlenwerte, die ich aus den π – Werten der vier Pyramidenviertel abgeleitet habe. Unser normales π spielt hierbei nicht die geringste Rolle!
Betrachten wir nun die vier verschiedenen Grundseitenlängen der π Systeme in der Einheit GE (siehe Tabelle 2).
| π – System | Grundseitenlänge |
| 3 1/7 | 168,0650449 GE |
| πantik | 168 GE |
| πphi | 168,1585392 GE |
| πphi – Partner | 167,9065937 GE |
| Summe | 672,1301778 GE |
| πD | 168,0325193 GE |
| Summe 4 x πD | 672,1300772 GE |
| Differenz | 1,006 x 10-4 GE |
Tab.2: π – Systeme und Grundseitenlängen
Zählt man die vier verschiedenen Grundseitenlängen zusammen, erhält man den Pyramidenumfang. Setzt man πD zur Berechnung der Grundseitenlänge ein und multipliziert mit 4, ergibt sich ein Durchschnittsumfang. Der Unterschied beider Umfänge beträgt 1,006 x 10-4 GE, das sind gerade einmal um die 14 mm! Ich interpretiere das als Bestätigung der bisherigen Berechnungen.
Die Cheopspyramide und die Bibel
Wie im Buch „Der Pyramiden – Code“ ab S. 110 ff. dargestellt, hatte sich in der Sintflutgeschichte um Noah gezeigt, dass bestimmte darin enthaltenen Zahlen, nämlich Zeitangaben, nach entsprechender Aufbereitung den Code für die Länge eines irdischen Jahres (365,242 Tage) bis auf drei Stellen hinter dem Komma genau enthalten.
Prof. Herbert Müller hat das in den Wismarar Diskussionspapieren der Universität Wismar übernommen:
„Dass es offenbar nicht unzulässig ist, in der Noah-Geschichte nach verschlüsselten Sach-Informationen zu suchen, wird im folgenden nach /BR, S. 110ff (BR = Bergmann / Rothe: Der Pyramiden – Code) dargestellt: Die Zeitangaben in der Noah-Geschichte /B,1.Mose,7/ sind in ihrem Nacheinander, wie die folgende Tabelle zeigt, skurril – so folgt z. B. auf den 2.,7., und 10. Monat erst der 1. Monat. Sie werden aber verständlich, wenn man sie als Codierung begreift, indem die jeweils 2. Zahl jeder Zeile als echter Bruch mit „1“ im Zähler verstanden wird.
- 17. Tag des 2. Monats = Sintflutbeginn 17 + ½ = 17,500000
- 17. Tag des 7. Monats = Araratlandung 17 + 1/7 = 17,142857
- nun Hinweis in Bibel: Gewässerabnahme bis auf 10. Monat
- 1. Tag des 10. Monats = Bergspitzen sichtbar 1 + 1/10 = 1,100000
- 1. Tag des 1. Monats = Wasser weggetrocknet 1 + 1/1 = 2,000000
- 27. Tag des 2. Monats = ganze Erde trocken 27 +1/2 = 27,500000
- Zwischensumme = 65,242857
- Multiplikation der beiden Zahlen vor dem Hinweis
- 17,5 x 17,142857 = 300,000000
- Gesamtsumme = 365,24285
Die Tabelle gibt die zugehörigen Dezimalzahlen an und zeigt, wie aus diesen Angaben eine Gesamtsumme entsteht, die erst im Zehntausendstel-Bereich von der heute bekannten äquinoktialen Jahreslänge (1 Jahr = 365,2422 Tage) abweicht – im Hinblick auf die für die Alten sehr wichtige Kalendrierung der Zeit offenbar eine Schlüsselzahl.“
Die erste Zahl der Liste – 17,5 – wird uns gleich an anderer Stelle der Bibel wieder begegnen.
In 1.Mose 5 heißt es: „Dies ist das Buch von Adams Geschlecht“.
„Und Adam war 130 Jahre alt und zeugte einen Sohn, ihm gleich und nach seinem Bilde, und nannte ihn Seth; und lebte danach 800 Jahre und zeugte Söhne und Töchter, dass sein ganzes Alter ward 930 Jahre, und starb.“
Auf diese Weise beschreibt die Bibel die Altersdaten der ersten zehn Bibelväter (siehe Tabelle 3).
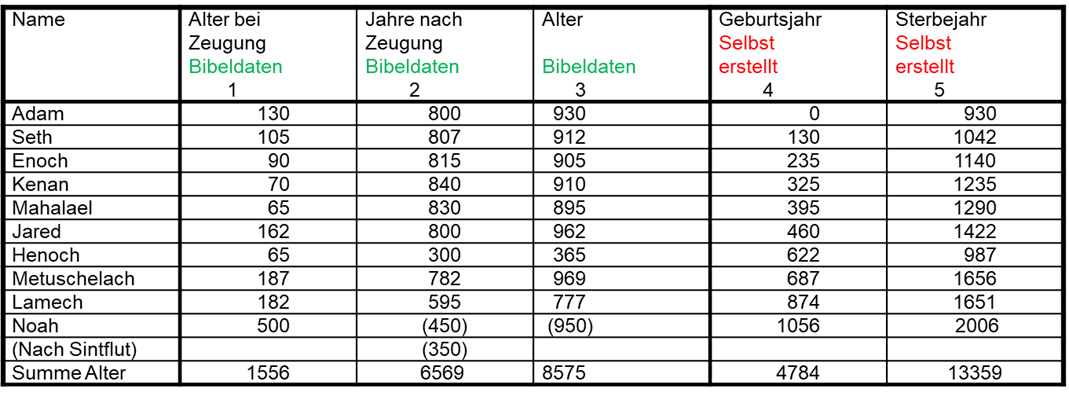
Tab.3: Die zehn Bibelväter
Die Zahlen der ersten drei Zahlenspalten stehen alle wortwörtlich offen in der Genesis. Die Zahlen der letzten beiden Zahlenspalten muss man selbst errechnen, sie sind also verborgen.
Zieht man von der Alterssumme der ersten Zahlenspalte das Noah – Alter ab, bekommt man eine neue Superzahl: 1056.
Teilt man nun 1056 durch 132/35, den Multiplikator von φ2 zur Zahl πD2 erhält man überraschenderweise die Höhe der Cheopspyramide in KE:
1056 : 132/35 = 280. Teilt man dies noch durch φ2, hat man die Pyramidenhöhe zu 106,9504831 GE. In Kurzform: 1056 : πD2 = hCheops in GE.
Wir betrachten nun die ersten drei Zahlenspalten in Tabelle 3, die offen in der Bibel stehen. Hier sind in der Noah – Zeile und eine Zeile darunter drei Zahlen in Klammern gesetzt. In 1.Mose 5 steht: “Noah war 500 Jahre alt und zeugte Sem, Ham und Japhet.“ Hat er Drillinge bekommen, waren es drei verschiedene Frauen oder vielleicht drei in der Tabelle fehlende Zahlen?
In 1. Mose 9 steht: „Noah aber lebte nach der Sintflut 350 Jahre, dass sein ganzes Alter ward 950 Jahre und starb.“
Die letzte Zahl aus 1.Mose 5 war 500, die letzte Zahl aus 1.Mose 9 war 950. Die Differenz ist 450.
Diese drei Zahlenwerte (350 Jahre, 450 Jahre und 950 Jahre) sind in Klammern stehend in der Tabelle ergänzt.
Addiert man nun alle Zahlen der Spalten 1 bis 3 ohne die drei Zahlen in Klammern, ergibt sich die Zahl 15 750. Die Addition der drei Zahlen in Klammern ergibt 1 750. Und 15 750 plus 1 750 ist 17 500.
Um diese weiteren Schlüsselzahlen zu deuten, schauen wir auf die Darstellung des Pyramidenfeldes von Gizeh aus dem Kapitel mit der königlichen Elle. Hier sind die Diagonalenparallelen eingezeichnet. Der Abstand der Diagonalen der Cheops – und der Chephrenpyramide beträgt 15,75 GE. Multipliziert mit 1000 ergibt das die 15 750 aus der Geschlechtertafel.
- Das Vierfache von 15,75 ist 63. Das ist die Maximalzahl an Plätzen auf dem äußeren Neutronenkreis in meinem Neuen Modell des Atomkerns (siehe eines der Folgekapitel).
- Das Fünffache von 15,75 ist 78,75, die Seitenlänge der Mykerinospyramide in GE.
- Das Achtfache von 15,75 ist 126, die Maximalanzahl von Neutronen vor dem Beginn der immerwährenden Radioaktivität.
- Das Zehnfache schließlich ist 157,5, die Seitenlänge der Chephrenpyramide in GE.
- Der Abstand der Diagonalen der Chephren – und der Mykerinospyramide beträgt 17,5 GE. Das Tausendfache davon führt uns zur Schlüsselzahl 17 500 aus der Geschlechtertabelle.
- Das Doppelte von 17,5 ist 35, der Nenner von 132/35.
- Das Vierfache von 17,5 ist 70, die Maximalzahl von Neutronen auf dem inneren Neutronenkreis.
- Das Neunfache von 17,5 ergibt 157,5, die Seitenlänge der Chephrenpyramide in GE.
- Das Sechzehnfache von 17,5 ist 280, die Höhe der Cheopspyramide in KE.
Alles nur Zufall?
Schauen wir nun noch die restlichen Altersdaten der Bibelväter in Tabelle 3 an. In der Zahlenspalte 5 in der sechsten Zeile finden wir die Zahl 1422, in der Zeile darüber steht 1290. 1422 – 1290 ergibt 132, den Zähler von πD2 . In Zahlenspalte 3 steht in Zeile 1 die Zahl 930, in Zeile 5 die Zahl 895. 930 – 895 ergibt 35, den Nenner von πD2.
Die Pyramidenhöhe von 280 KE erhält man mit folgender Zahlenoperation:300 (Spalte 2, Zeile 7) + 162 (Spalte 1, Zeile 6) – 182 (Spalte 1, Zeile 9) = 280
Die Rechnung 595 (Spalte 2, Zeile 9) – 65 (Spalte 1, Zeile 5) – 90 (Spalte 1, Zeile 3) ergibt 440, die Grundseitenlänge in KE.
Rechnet man 325 (Spalte 4, Zeile 4) + 395 (Spalte 4, Zeile 5) erhält man 720, sie Summe aus 280 und 440.
Die Rechnung 2006 (Spalte 5, Zeile 10) – 840 (Spalte 2, Zeile 4) – 830 (Spalte 2, Zeile 5)) ergibt 336, die doppelte Grundseitenlänge in GE.
Addiert man nun 280 + 440 +336 ergibt sich die Superzahl 1056.
Handelt es sich hier um eine reine Geschlechtertafel oder eher um eine Codetabelle?
Mittelwertbildung
Hier nun die mathematische Herleitung von πD und πD2 mittels fortschreitender Mittelwertbildung. Es hatte sich gezeigt, dass man die Höhe der Cheopspyramide in GE erhält, wenn man die Schlüsselzahl 1056 durch πD2 teilt. πD2 selbst ist das Produkt von zwei π – Partnern. Jetzt nehmen wir als den ersten π – Partner 3 1/7. Teilen wir 1056 durch 3 1/7 erhalten wir 336, das ist die doppelte Seitenlänge der Cheopspyramide in der Einheit GE. Teilen wir 336 durch die Höhe der Cheopspyramide in GE, ergibt sich der π – Partner von 3 1/7, nämlich πantik. Addieren wir beide π – Partner (3 1/7 + πantik) erhalten wir 6,28449793. Teilt man diese Zahl durch 2 erhält man 3,142248965.
Fasst man das als einen dritten neuen π – Wert auf, kann man 1056 durch den neuen π – Wert teilen und erhält 336,0650323. Teilt man diese Zahl wie bei der Ermittlung von πantik durch die Höhe der Cheopspyramide in GE, ergibt sich ein vierter neuer π – Wert, nämlich 3,142248847, wobei es sich beim dritten und vierten neuen π – Wert wiederum um π – Partner handelt, deren Produkt πD2 ergibt.
Nun addieren wir den dritten und vierten neuen π – Wert und wir bekommen 6,284497812. Teilen wir diese Zahl wieder durch 2, ergibt sich unser Durchschnitts – Pi zu 3,142248906. Bereits nach der zweiten Mittelwertbildung hat sich also πD ergeben.
Mathematisch gesehen ist die fortschreitende Mittelwertbildung für ein beliebiges Zahlenpaar nichts Besonderes. Die Multiplikation des Zahlenpaares ergibt eine Produktkonstante. Bei der Mittelwertbildung wird der eine Partner der Produktkonstante etwas kleiner, der andere dafür etwas größer, so dass immer dasselbe Ergebnis, nämlich die Produktkonstante, herauskommt. Irgendwann wird immer der Punkt erreicht, wo beide Partner gleich sind und deren Quadrat die Produktkonstante ergibt.
Das Besondere an der Produktkonstante πD2 ist deren Zusammenhang mit der Zahl 1056.
Tabelle 4 zeigt den Zusammenhang für die π – Partner auf. Warum aber führt uns die Schlüsselzahl 1056 hier hin?. Dazu setzen wir die Seitenlängen der Cheops – und der Chephren – Pyramide ins Verhältnis (168 GE : 157,5 GE = 1,0666…). Genau dieses Verhältnis ergibt sich auch, wenn man das c„ und das h unserer Tonleiter ins Verhältnis setzt (528 : 495 = 1,0666…). Jetzt gehen wir eine Oktave höher (1056 : 990 = 1,0666…). Es ergibt sich der begründete Verdacht, dass es sich bei der Zahl 1056 um eine akustische Frequenz handeln könnte, auf die wir aufmerksam gemacht werden sollen.
| 1056 | : | πD2 | = | hCheops |
| 1056 | : | π – Wert1 | = | 2 x sCheops |
| 2 x sCheops | : | π – Wert2 | = | hCheops |
Tab. 4: 1056 und πD2
Die Grundformel
Die Formel aus Tabelle 4, Zeile 1 läßt sich auch schreiben als
1056 = πD2 x hCheops.
Da πD2 das Produkt zweier π – Partner ist, gilt in unserem Beispiel und auf die vier Pyramidenviertel bezogen die Rechenvorschrift
π1 x π2 = π3 x π4 = konstant = πD2
mit π1 = 3 1/7, π2 = πantik, π3 = πphi und π4 = πphi – Partner.
In der Mathematik gibt es den Begriff der Kennzahl oder Kenngröße, bezeichnet als Z. Hier wäre Z = 1056. In Formeln ausgedrückt:
ZCheops = π1 x π2 x h = πD2 x h = 1056
ZCheops = 132/35 φ2 x 280/φ2 = 1056
Daraus abgeleitet gilt folgende Rechenvorschrift:
ZCheops/π1 = π2 x h = 2s 2s/h = π2
1056 / 3 1/7 = 336 336/(280/φ2) = πantik
In Worten ausgedrückt: Kennziffer geteilt durch 3 1/7 ergibt die doppelte Seitenlänge, diese geteilt durch die Höhe ergibt den zweiten π – Wert.
Die Kennziffer der Chephrenpyramide ist ZChephren = 1056 : 1,0666… = 990. Wendet man πD2 x h auf die Kennziffer der Chephrenpyramide an, erhält man die Zahl 262,5 als Höhe h. Da wir mit dem Neigungswinkel der Cheopspyramide gerechnet haben, ist das natürlich nicht die ursprüngliche Höhe der Chephrenpyramide. Es ist die Höhe der Gipfelplattform der Cheopspyramide. Dasselbe Ergebnis von 262,5 bietet die Rechnung 280 : 1,0666… .
Teilen wir die Kennziffer der Chephrenpyramide 990 durch 3 1/7, erhalten wir ihre doppelte Seitenlänge zu 315 GE. Die Seitenlänge selbst beträgt dann 157,5 GE.
Die Rechnung 315 : (262,5/φ2) ergibt folgerichtig den zweiten π – Wert πantik.
Die Grundformel lautet π1 x π2 x h = Z
Mit der Rechenvorschrift π1 x π2 = πD2
Man kann das auf mehrere geometrische Sachverhalte anwenden:
Zweidimensional: Rechteck s1 = πD2 s2 = h Z = Fläche
Ein Rechteck hat zwei verschieden lange Seiten s1 und s2, die Kennzahl wäre dann die Fläche.
Dreidimensional: z.B. Kubus s1 = π1 s2 = π2 s3 = h Z = Volumen
Ein Kubus hat drei verschiedene Seitenlängen, die Kennzahl entspräche hier dem Volumen.
Dreidimensional: z.B. Pyramide s1 = π1 s2 = π2
s3 = π3 s4 = π4 h = h
Mit der Rechenvorschrift π1 x π2 = π3 x π4 = πD2
Damit sind die vier verschiedenen Pyramidenviertel und die Pyramidenhöhe gekennzeichnet. Im Fall einer Pyramide stehen Kennzahl und Höhe für die absolute Größe des Bauwerks, die verschiedenen π – Werte bestimmen die Neigungswinkel an der Basis.
Was lässt sich mit dieser Grundformel für die Cheopspyramide anfangen?
π1 x π2 = πD2 = 132/35 φ2 wurde von den Erbauern so festgesetzt und verweist mit πD2 auf eine der Wissenschaft bis jetzt noch unbekannte Konstante.
πantik und 3 1/7 könnten für den Raum und die Zeit stehen. Der berühmte Seher und Prophet Nostradamus schreibt von 1002 Propheten, die für die Zeit stehen.
3 1/7 lässt sich auch schreiben als 3,142857. Addiert man 142 + 857 erhält man 999. Die 3 dazu addiert ergibt 1002.
Die π – Partner πphi und πphi – Partner lassen sich bisher noch nicht einordnen, wobei πphi für den geometrischen Tatbestand der Schnittpunkte der Sinus – , der Cosinus – , der Tangens – und der Cotangenskurve steht.
Die Pyramidenhöhe von 280 KE könnte auf den Elektronenbereich hinweisen. In meinem neuen Atommodell besteht ein Elektron aus insgesamt 28 Teilen. Die Grundwährung ist dort das Achtundzwanzigstelelektron. Somit stünde die Höhe der Cheopspyramide in Resonanz zu den Elektronen.
Die Kennziffern der drei Pyramiden (1056 = Cheops, 990 = Chephren, 495 = Mykerinos) stehen in Beziehung zu Tönen unserer Tonleiter (1056 Hz = c„`, 990 Hz = h„, 495 Hz = h). Zusätzlich sind hier in einer einzigen Ziffer die äußeren Gesamtabmessungen der Bauwerke festgelegt.
Sollte es sich bei den Zahlen 1056, 990 und 495 tatsächlich um akustische Trägerfrequenzen handeln, sind alle Objekte angesprochen, die diese Frequenzen in sich tragen, sie sind resonant zu 1056 Hz, 990 Hz oder 495 Hz. Auf diese Trägerfrequenzen lassen sich beliebig viele weitere Frequenzen aufmodulieren. Je nach Intensität (niedrig = Anregung, mittel = Schütteln, z.B. Erdbeben, hoch = Zerstörung, z.B. Explosion) könnte von fast nichts bis zu riesengroßer Zerstörung alles passieren. In dieser Sicht wären die drei Pyramiden sicherlich als fortschrittliche Waffensysteme anzusehen.
Was bedeutet der über Archimedes hinaus erweiterte Bereich für π?
Er führt zur Grundformel, führt zur Rekonstruktion des Bauplans der Cheopspyramide und des gesamten Pyramidenfelds von Gizeh und er führt auf direktem Weg in die Atomphysik.
Als praktische Konsequenz könnte von extrem nützlich bis zur totalen Zerstörung alles möglich sein. Aber dazu muss man erst einmal die Theorie in die Praxis umsetzen können. So weit sind wir (glücklicherweise?) noch lange nicht!
