Die zwei Elektronenringe Teil 2

Verlässt ein Elektron die Elektronenhülle, entsteht ein positiv geladenes Ion. In diesem Fall schließen sich die 28 Achtundzwanzigstelelektronen zu einem Elektron zusammen und ein Beobachter misst eine einzige Elementarladung e^–. Ein Elektron kann also nicht mit einer gebrochenen Elementarladung außerhalb der Elektronenhülle eines Atoms existieren. Im umgekehrten Fall, wenn also ein Atom ein Elektron in seine Hülle aufnimmt – es entsteht ein negativ geladenes Ion – spaltet sich das Elektron in seine 28 Achtundzwanzigstelelektronen auf und nimmt die entsprechenden Plätze auf den beiden Ringen ein.

Bei der neuen Einteilung des Periodensystems waren die Elemente Lithium und Beryllium sowie Natrium und Magnesium aus den Zweiergruppen heraus in die Achtergruppen hineingerückt. Einen stichhaltigen Beweis dafür liefern die Ionisierungsenergien.

In Tab. 1 sind die Ionisierungsenergien I₁ – I₇ der ersten 18 chemischen Elemente aufgetragen. Die Werte entstammen den Tabellen des NIST 2020 (National Institut for Science and Technology aus den USA) und sind auf eine Nachkommastelle gerundet.

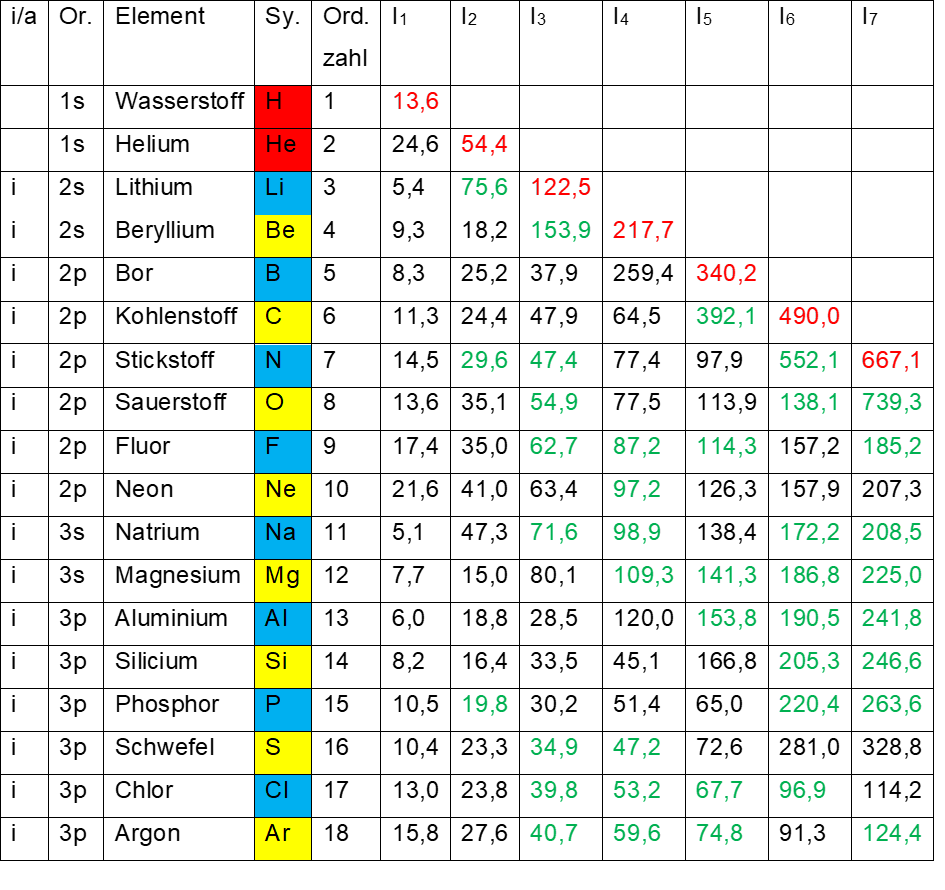
Tab. 1: Ionisierungsenergien I₁ – I₇ der Elemente 1 – 18
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

Ein einziges Elektron aus dem Element Nummer 3, Lithium, herauszulösen, erfordert lediglich die Energie von 5,4 eV. Die Elektronenachtundzwanzigstel von Lithium befinden sich in den blauen Sektoren für die ungeraden Elemente. Das zweite und das dritte herauszulösende Elektron von Lithium aber hat seine Plätze in den roten Bezirken (Helium – und Wasserstoffzustand), man benötigt dafür 75,6 eV und 122,5 eV, eine eminent höhere Energiemenge als für das erste herauszulösende Elektron.

Bis hierhin hat die Sache allerdings einen Haken. In Tab. 1 haben die Ionisierungsenergien verschiedene Farben. Die Farbe schwarz steht für tatsächlich gemessene Werte. In grüner Farbe sind intra – oder extrapolierte Werte angegeben, die Farbe rot steht für rein theoretisch berechnete Werte. Bei I₂ (grün) und I₃ (rot) von Lithium handelt es sich also nicht um tatsächliche Messwerte.

Das nächste Element, Nummer 4, Beryllium, hat das erste Elektron in den gelben Sektoren, das zweite in den blauen Sektoren, das dritte in den roten Bezirken. I₁ beträgt geringe 9,3 eV, I₂ 18,2 eV, bedeutend weniger als die 75,6 eV im Fall der Herauslösung aus den roten Bezirken des Lithium. I₃ bei Beryllium dagegen beträgt gewaltige 153,9 eV, da hier wieder auf die roten Bezirke zugegriffen werden muss. Allerdings ist I₃ hier kein tatsächlicher Messwert. Da er die Farbe grün aufweist, ist er intra – oder extrapoliert.

Diese Situation ändert sich beim nächsten chemischen Element Bor. Hier sind I₁ – I₄ echte Messwerte. Bor hat die Ordnungszahl 5 und somit fünf Elektronen. Das erste herauszulösende Elektron befindet sich in den blauen Sektoren (ungerade) mit einer vergleichsweise bescheidenen I₁ von 8,3 eV. Für das aus den gelben Sektoren herauszulösende zweite Elektron (gerade, Berylliumzustand) benötigt man schon 25,2 eV. Das dritte herauszulösende Elektron stammt wieder aus den blauen Sektoren (ungerade, Lithiumzustand) und erfordert 37,9 eV. Das vierte herauszulösende Elektron gehört in die roten Bezirke rot 2 und rot 4 des inneren und des äußeren Elektronenrings (gerade, Heliumzustand). Hierfür braucht es immense 259,4 eV. Hier sieht man erstmals in Form tatsächlich gemessener Werte diese charakteristische Kante im Periodensystem.

Dass Lithium und Beryllium in die erste Achtergruppe und nicht in die Zweiergruppe von Wasserstoff und Helium gehören, zeigen auch die ersten Ionisierungenergien dieser vier Elemente. Wasserstoff hat eine I₁ von 13,6 eV (allerdings nur theoretischer Wert), Helium hat eine I₁ von 24,6 eV. Dagegen betragen die I₁von Lithium und Beryllium vergleichsweise bescheidene 5,4 und 9,3 eV. Die folgenden Elemente Kohlenstoff (11,3 eV), Stickstoff (14,5 eV), Sauerstoff (13,6 eV), Fluor (17,4 eV) und Neon (21,6 eV) haben leicht ansteigende Werte, die aber nicht die 24,6 eV von Helium erreichen.

Im bisher geltenden Standardmodell befinden sich die Elektronen von Wasserstoff und Helium auf der 1s – Schale, die von Lithium und Beryllium auf der 2s – Schale, wobei die 2s – Schale ein viel niedrigeres Energieniveau als die 1s – Schale besitzt. Die folgenden Elemente Bor bis Neon haben ihre Elektronen auf der 2p – Schale und besitzen ein ähnliches Energieniveau wie die 2s – Schale.

Bei Bor hatte sich gezeigt, dass man, um in den Heliumzustand zu kommen, 259,4 eV aufwenden muss gegenüber 37,9 eV für den Lithiumzustand. Im neuen Modell des Periodensystems ist diese energetische Kante gut erklärbar, da hier von den blauen in die roten Sektoren gewechselt wird. Diese Erklärung trifft natürlich auch für das Standardmodell zu (die zwei Elektronen der 2s – Schale werden entfernt und das dritte zu entfernende Elektron gehört der 1s – Schale an, also findet auch hier ein Schalenwechsel statt..

Im Standardmodell stehen Lithium und Beryllium als Zweiergruppe (= 2s – Schale) unterhalb von Wasserstoff. Deshalb sollte es als Trennung der 2p – Schale von der 2s – Schale auch solch eine energetische Kante geben. Geht man wie bei Bor vor (drei Elemente vor Helium), muss man bei Stickstoff (drei Elemente vor Beryllium) nachschauen. Für den Borzustand müssen drei Elektronen entfernt werden, I₃ beträgt 47,4 eV (grün = intra – oder extrapolierter Wert). I₄für den Berylliumzustand beträgt 77,4 ev (schwarz, tatsächlicher Messwert). Hier besteht eine Differenz von 30 eV gegenüber 255,5 eV beim Heliumzustand des Bor. Eine solche energetische Kante ist für das Paar Lithium und Beryllium nicht nachweisbar, was klar dafür spricht, dass diese beiden Elemente nicht in eine Zweiergruppe wie im Standardmodell gehören. Entfernt man beim Stickstoff ein weiteres Elektron, gelangt man in den Lithiumzustand und benötigt 97,9 eV (schwarz, Messwert) dafür. Hier findet sich wieder die angesprochene energetische Kante, denn um in den Heliumzustand zu kommen, braucht es jetzt 552,1 ev (grün, intra – oder extrapolierter Wert).

Im neuen Modell des Periodensystems stehen auch Natrium und Magnesium nicht mehr in den Zweiergruppen, sondern in der zweiten nach rechts geschriebenen Achtergruppe. Das wird durch ihre ersten Ionisierungsenergien bestätigt, die 5,1 eV (Natrium) und 7,7 eV (Magnesium) betragen, ähnliche Werte wie Lithium (5,4 eV) und Beryllium (9,3 eV). Sie sind damit weit weg vom Heliumwert (24,6 eV) aus der roten Zweiergruppe.

Wenn man die ersten beiden nach rechts geschriebenen Achtergruppen miteinander vergleicht, zeigt sich ein weitgehend identisches Szenario mit dem sprunghaften Anstieg von I₁.

Betrachtet man nun das Ende der ersten Achtergruppe (Neon, I₁ = 21,6 eV) und den Beginn der zweiten Achtergruppe (Natrium, I₁ = 5,1 eV), zeigt sich, dass es sich tatsächlich um zwei verschiedene Schalen handeln muss. Den Beweis hierfür liefern die Ionisierungsenergien ab I₂. Bei den Elementen Natrium und Magnesium muss beim zweiten und dritten herauszulösenden Elektron nicht auf die roten Bezirke zugegriffen werden, sondern auf die gelben und blauen Sektoren der ersten Achtergruppe der Elemente (Neon und Fluor). Ganz deutlich aber ist die Situation beim Aluminium, dem dritten Element dieser Achtergruppe. Hier können die drei Elektronen der eigenen Achtergruppe entfernt werden und demzufolge beträgt I₃ vergleichsweise bescheidene 28,5 eV gegenüber 80,1 eV beim Magnesium, dessen drittes herauszulösendes Elektron der Neonschale angehört. I₄ beim Aluminium beträgt dementsprechend auch 120,0 eV, da auch hier jetzt auf den Neonzustand zugegriffen wird. Alle in diesem Abschnitt angeführten Energiewerte sind echte Messwerte.

Im Standardmodell haben Natrium und Magnesium ihre Elektronen auf der 3s – Schale, die Elemente Aluminium bis Argon auf der 3p – Schale. Ihre Energieniveaus sind ähnlich wie die der 2s – und der 2p – Schale.

Auch hier findet sich keine klar erkennbare energetische Kante zwischen der 3s – und der 3p – Schale. Diese tritt erst auf, wenn man sich bei allen acht Elementen der zweiten nach rechts geschriebenen Achtergruppe (Natrium – Argon) in den Neonzustand begibt.(sechs tatsächliche Messwerte, zwei inter – oder extrapolierte Werte, siehe Tab.1). Auch das spricht klar dafür, dass die Elemente Natrium und Magnesium in eine Achtergruppe gehören und nicht in eine Zweiergruppe wie im Standardmodell.

In Tab.2 sind die entsprechenden Ionisierungsenergien der Elemente 17 – 36 aufgetragen. Beim Vergleich der I₁ – Werte für Chlor (13,0 eV) und Argon (15,8 eV) am Ende der zweiten nach rechts geschriebenen Achtergruppe mit den Werten für Kalium (4,3 eV) und Calcium (6,1 eV) der zweiten roten Zweiergruppe stößt man wieder auf so eine ausgeprägte energetische Kante im Periodensystem.

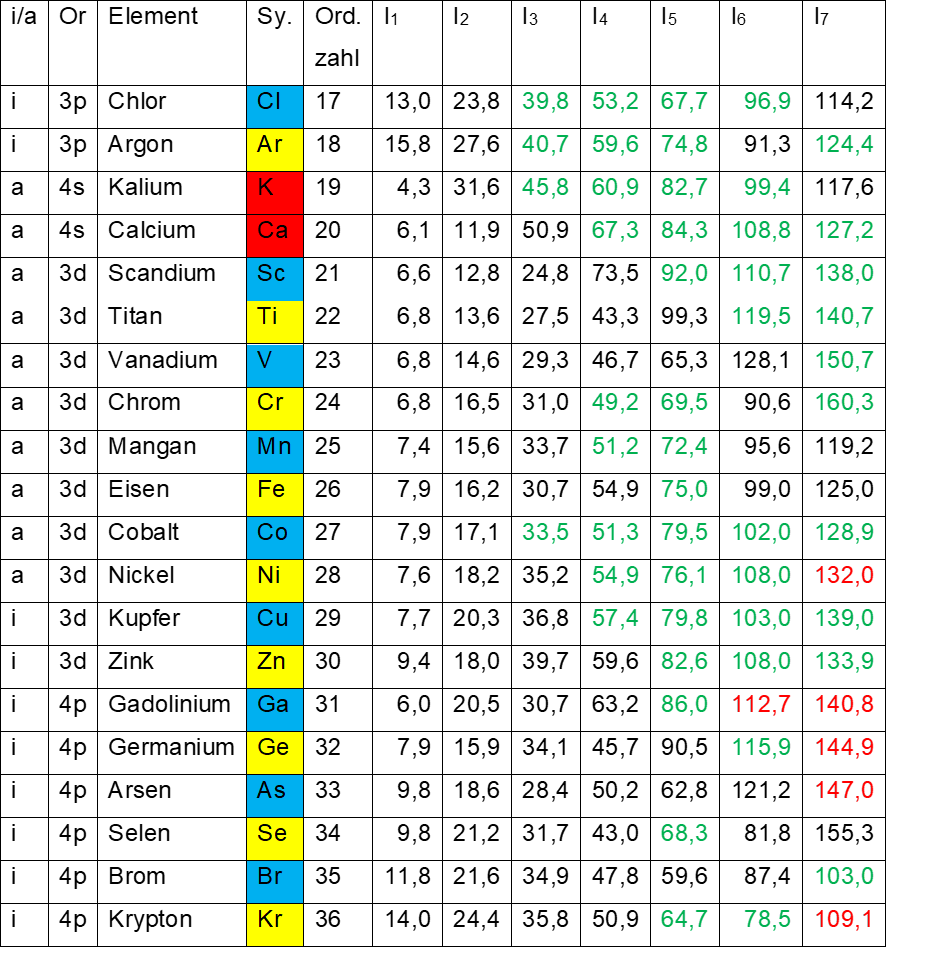
Tab. 2: Ionisierungsenergien I₁ – I₇ der Elemente 17 – 36
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

Die folgenden Elemente Scandium bis Nickel gehören der ersten nach links geschriebenen Achtergruppe an. Ihre I₁ – Werte bewegen sich im engen Bereich 6,6 eV bis 7,9 eV und damit in einem ähnlichen Bereich wie Kalium und Calcium, was dafür spricht, dass sich ihre Elektronenachtundzwanzigstel auf dem leichter zugänglichen äußeren Elektronenring befinden. Um hier ein Elektron herauszulösen, muss wesentlich weniger Energie aufgewendet werden als beim inneren Elektronenring.

Betrachtet man die Übergänge Scandium (blau) – Calcium (rot) – Kalium (rot) – Argon (gelb), stößt man wiederum auf energetische Kanten. Für das erste aus Scandium herauszulösende Elektron benötigt man geringe 6,6 eV. Das zweite Elektron von Scandium befindet sich in rot 2 und rot 4 des äußeren Elektronenrings. Hierfür werden 12,8 eV benötigt, also etwa doppelt so viel wie beim ersten Elektron. Das dritte herauszulösende Elektron von Scandium befindet sich in den Bezirken rot 1 und rot 3 des äußeren Elektronenrings. Hier braucht es mit 24,8 eV fast wieder die doppelte Energiemenge. Das vierte herauszulösende Elektron von Scandium befindet sich in den gelben Sektoren des inneren Elektronenrings (Argonzustand). Jetzt werden sogar 73,5 eV benötigt, also fast die dreifache Energiemenge.

Das gleiche Spiel findet man beim folgenden Element Titan. Um vom Kaliumzustand (43,3 eV) zum Argonzustand zu gelangen, braucht es 99,3 eV. Auch beim folgenden Element Vanadium ist das zu sehen. Um zum Kaliumzustand zu gelangen, muss 65,3 eV aufgewendet werden, für den Argonzustand braucht es dann aber 128,1 eV. Alle in diesem Abschnitt angeführten Energiewerte sind tatsächlich ermittelte Messwerte.

Es folgen die Elemente Kupfer (29) bis Krypton (36). Deren I₁ – Werte weisen wieder den sprunghaften Anstieg der nach rechts geschriebenen Achtergruppen auf. Zum Beginn (Kupfer 7,7 eV und Zink 9,4 eV) befinden sich die I₁ – Werte im Bereich der Werte für Cobalt (7,9 eV) und Nickel (7,6 eV). Am Ende findet sich dann aber ein erheblicher Anstieg zu Brom (11,8 eV) und Krypton (14,0 eV).

Um von dieser nach rechts geschriebenen Achtergruppe in den Nickelzustand der vorangegangenen nach links geschriebenen Achtergruppe zu kommen, findet sich wieder eine ausgeprägte energetische Kante. I₁ für Kupfer beträgt 7,7 eV, I₂ (Nickelzustand) beträgt 20,3 eV. Beim Zink finden sich die Werte 18,0 eV (Kupferzustand) gegenüber 36,8 eV (Nickelzustand). Auch beim darauf folgenden Gadolinium kann man das beobachten. Für den Kupferzustand müssen 30,7 eV aufgewendet werden, für den Nickelzustand dagegen 63,2 eV. Auch beim folgenden Germanium ist die Situation so: 45,7 eV (Kupferzustand) gegenüber 90,5 eV (Nickelzustand). Auch beim fünften Element dieser Achtergruppe geht es so weiter: 62,8 eV (Kupferzustand) versus 121,2 eV. Es folgt das Element Selen mit 81,8 eV (Kupferzustand) gegenüber 155,3 eV (Nickelzustand). Bis hierhin handelt es sich bei den angeführten Energiewerten um tatsächlich ermittelte Messwerte.

Das siebte Element dieser Achtergruppe ist Brom. Hier finden sich 103,0 eV (Kupferzustand, inter – oder extrapolierter Wert) versus 192,6 eV (Nickelzustand, Messwert). Das letzte Element der Achtergruppe ist Krypton mit 125,8 eV (Kupferzustand, Messwert) gegenüber 223,0 eV (Nickelzustand, inter – oder extrapolierter Wert).

Diese energetische Kante lässt sich also vom ersten bis zum letzten Element dieser nach rechts geschriebenen Achtergruppe verfolgen. Im Standardmodell dagegen befinden sich die Elektronen der Elemente Scandium (21) bis Zink (30) auf der 3d – Schale, die der Elemente Gadolinium (31) bis Krypton (36) auf der 4p – Schale. Einen Übergang Nickel / Kupfer gibt es hier nicht. Auch eine energetische Kante zwischen der 3d – und der 4p – Schale (Zink – Gadolinium) existiert nicht.

Im Periodensystem folgen nun die Elemente der roten Bezirke Rubidium (37) und Strontium (38). Darauf folgt die nach links geschriebene Achtergruppe Yttrium (39) bis Palladium (46). Tab. 3 zeigt die Ionisierungsenergien von Brom (35) bis Xenon (54).

I₁ beträgt bei Rubidium geringe 4,2 eV und bei Strontium ebenso geringe 5,7 eV. Das spricht dafür, dass deren Elektronenachtundzwanzigstel sich in den Bezirken rot 1 und rot 3 (Rubidium) bzw. rot 2 und rot 4 (Strontium) des äußeren Elektronenrings befinden. Will man bei beiden Elementen in die nächst niedrige Schale gelangen (Kryptonzustand), muss man bei Rubidium schon 27,3 eV (I₂) aufwenden, bei Strontium 42,9 eV (I₃). Es handelt sich wieder um eine dieser energetischen Kanten des Periodensystems.

Die nächsten zu erwartenden Kanten wären an den Stellen zu erwarten, wo man von der nach links geschriebenen Achtergruppe Yttrium (39) bis Palladium (46) zum Strontiumzustand (38) und danach zum Kryptonzustand (36) gelangt.

Leider zeigt Tab. 3 in diesen Bereichen viele grüne (intra – oder extrapolierte) und rote (theoretische) Werte an, so dass man nur auf wenige tatsächlich gemessene Werte zurückgreifen kann.

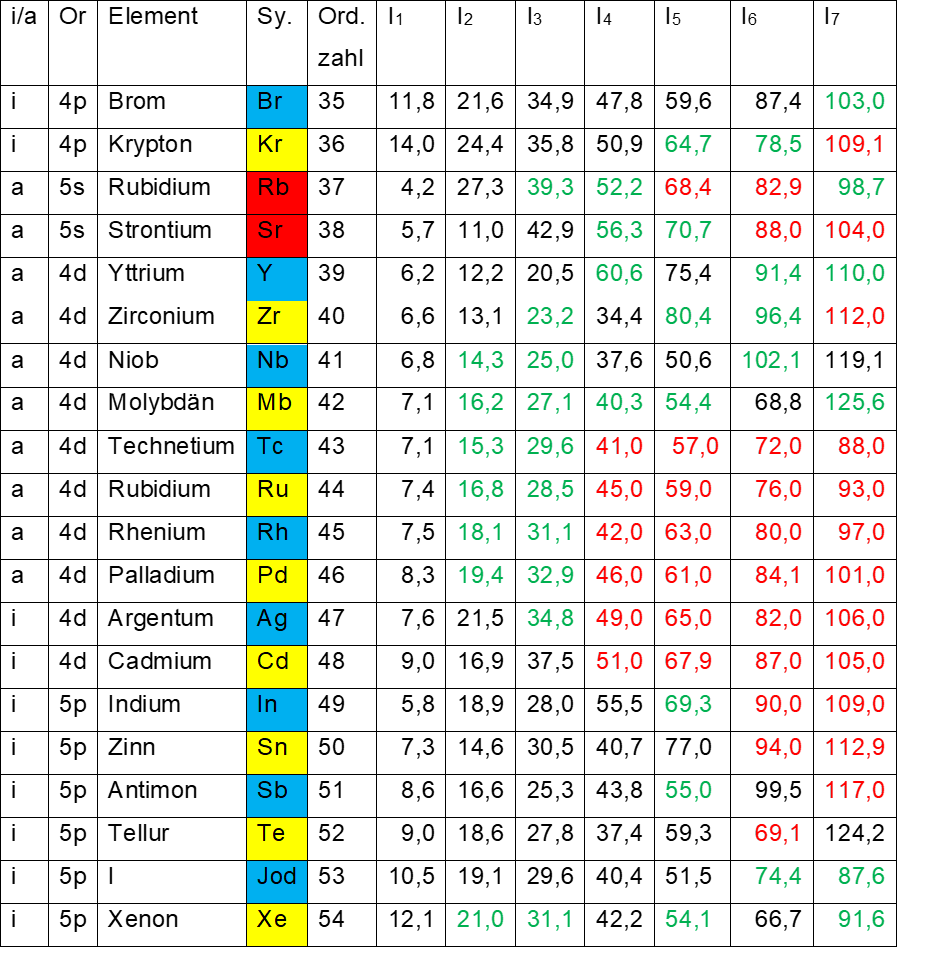
Tab. 3: Ionisierungsenergien I₁ – I₇ der Elemente 35 – 54
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

Will man beim Yttrium das zweite Elektron entfernen (Strontiumzustand), braucht es vergleichsweise geringe 12,2 eV (Messwert). Das dritte zu entfernende Elektron (Rubidiumzustand) benötigt 20,5 eV (Messwert), für den Kryptonzustand sind 60,6 eV (intra – oder extrapolierter Wert) aufzuwenden, für den Bromzustand sogar 75,4 eV, was den vorangegangenen intra – oder extrapolierten Wert (60,6 eV) bestätigt.

Um beim Zirconium (40) zum Strontiumzustand zu kommen, braucht es 23,2 eV (grün), für den Kryptonzustand 80,4 eV (grün).

Um zum Strontiumzustand zu gelangen, muss man bei der Achtergruppe Yttrium (39) bis Palladium (46) keine sehr hohen Energiemengen aufwenden, so dass diese energetische Kante nicht sehr ausgeprägt ist.

Will man jedoch zum Kryptonzustand vordringen, braucht es weitaus größere Energiemengen, wodurch diese Kante wieder ziemlich deutlich hervortritt.

Die nächste Achtergruppe Argentum (47) bis Xenon (54) ist nach rechts geschrieben, es handelt sich hier um den inneren Elektronenring. Hier findet sich ebenfalls eine sehr ausgeprägte energetische Kante, die sich sogar fast durchweg mit Messwerten belegen lässt.

Schon beim ersten Element Argentum findet sich ein energetischer Sprung von 7,6 eV (I₁) zu 21,5 eV (I₂, Palladiumzustand). Für Cadmium (42) beträgt der Sprung 16,9 eV zu 37,5 eV, für Indium 28,0 eV zu 55,5 eV, für Zinn 40,7 eV zu 77,0 eV, für Antimon 55,0 eV (grün) zu 99,5 eV, für Tellur 69,1 eV (rot) zu 124,2 eV, für Jod 87,6 eV (grün) zu 150,8 eV und für Xenon 106,0 zu 179,8 eV.

Im Standardmodell befinden sich die Elektronen der Elemente Yttrium (39) bis Cadmium (48) auf der 4d – Schale. Einen Übergang Argentum / Palladium gibt es hier wiederum nicht.

Im Periodensystem folgen jetzt die beiden Elemente in den roten Bezirken rot 1 und rot 3 (Caesium, 55) bzw. rot 2 und rot 4 (Barium, 56) auf dem äußeren Elektronenring (siehe Tab.4).

Die zu erwartende energetische Kante Caesium / Xenon lässt sich für Caesium (3,9 eV zu 23,2 eV) und Barium (10,0 eV zu 35,8 eV) gut darstellen und mit tatsächlich gemessenen Werten auch unterlegen.

Geht man jedoch in die nächste Achtergruppe (Lanthan bis Gadolinium), liegen für Lanthan noch drei Messwerte vor. Eine Kante von Lanthan zu Barium gibt es nicht, die Kante Caesium / Xenon lässt sich zwar vermuten, aber nicht mehr mit tatsächlich gemessenen Werten verifizieren. Ab jetzt gibt es jede Menge von grünen und roten Werten.

Auch eine Kante zwischen Gadolinium und Terbium lässt sich nicht erkennen. Auch dann nicht, wenn man die grünen Werte mit einbezieht. Aber hier ist auch keine Kante zu erwarten, denn alle Elemente von Lanthan bis Lutetium (Lanthaniden) haben ihre Elektronenachtundzwanzigstel auf dem gut zugänglichen äußeren Elektronenring.

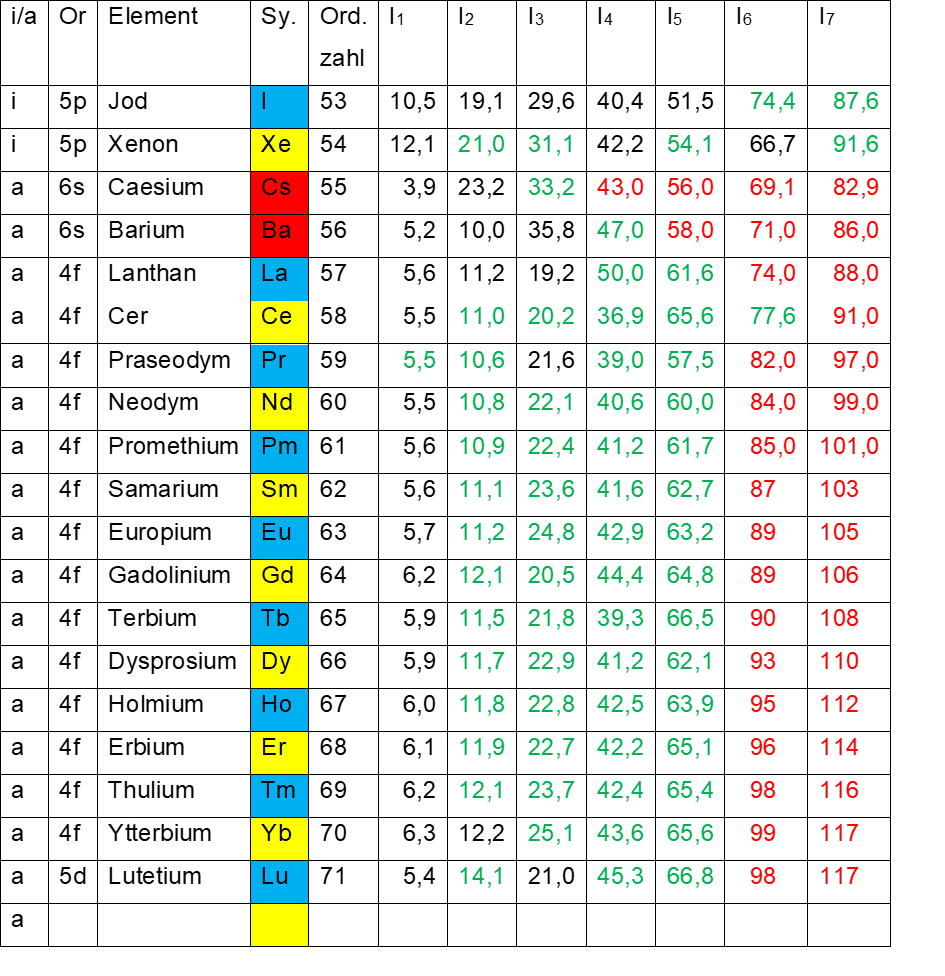
Tab. 4: Ionisierungsenergien I₁ – I₇ der Elemente 53 – 71
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

Im Standardmodell befinden sich die Elektronen von Caesium und Barium auf der 6s – Schale, die folgenden Lanthaniden haben die ersten 14 Elektronen auf der 4f – Schale. Da die Gruppe der Lanthaniden aber 15 Elemente umfasst, befindet sich das Elektron des Lutetium (fünfzehntes und letztes Element der Lanthaniden) auf der 5d – Schale.

Tab. 5: Ionisierungsenergien I₁ – I₇ der Elemente 72 – 86
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

In meinem neuen Modell des Periodensystems folgen nach Lutetium vier Lücken, die auch auf den Elektronenringen nachweisbar sind (siehe Tab. 4 und 5). Nach Lutetium gibt es auf dem äußeren Elektronenring eine ein Element umfassende Lücke in den gelben Sektoren (gerade), wo zwar Platz für Elektronenachtundzwanzigstel ist, sich dort aber keine befinden (siehe Tab. 4).

Es folgen zwei weitere Elemente – Lücken. Die roten Bezirke des äußeren Elektronenrings sind jetzt voll besetzt, so dass sich diese beiden Lücken zwangsläufig in den roten Bezirken des inneren Elektronenrings befinden.

Danach geht es weiter mit einer Elementen – Lücke auf dem äußeren Elektronenring in den blauen Sektoren (ungerade). Darauf folgt eine Gruppe aus sieben Elementen, ebenfalls auf dem äußeren Elektronenring (Hafnium bis Platin, siehe Tab.5).

Das letzte Lanthaniden – Element Lutetium vor der Vierer – Lücke besitzt mit 5,4 eV die geringste erste Ionisierungsenergie dieser Gruppe, so dass manche Wissenschaftler zweifeln, ob Lutetium an der richtigen Stelle des Periodensystems steht.

Ebenso wie die Lanthaniden ist die Siebenergruppe Hafnium – Platin nach links geschrieben (äußerer Elektronenring). Die erste Ionisierungsenergie jedes Elements dieser Siebenergruppe (6,8 eV, Hafnium bis 9,0 eV, Platin) ist geringgradig höher als die der Lanthaniden. Eine energetische Kante zwischen Lutetium und Hafnium existiert nicht und ist auch nicht zu erwarten, da sich die Elemente Lanthan (57) bis Platin (78) alle auf dem äußeren Elektronenring befinden.

Es folgt jetzt die nach rechts geschriebene Achtergruppe Gold (79) bis Radon (86). Hier finden sich wieder höhere erste Ionisierungsenergien mit ihren typischen sprunghaften Verläufen.

Auch hier gibt es zwischen Gold (79) und Platin (78) eine energetische Kante, die diesmal aber weitaus geringer ausgeprägt ist (siehe Tab.5) und sich größtenteils mit Messwerten unterlegen lässt. I₁ beträgt beim Gold 9,2 eV, I₂ 20,2 eV (Platinzustand). Beim Quecksilber (80) finden sich 18,8 eV versus 34,5 eV (Platinzustand), beim Thallium 29,9 eV versus 51,1 eV (Platinzustand). Für die restlichen Elemente dieser Achtergruppe existieren nur noch grüne oder rote Werte.

Im Standardmodell befinden sich die Elektronen der Elemente Lutetium (71) bis Quecksilber (80) auf der 5d – Schale., wohingegen in meinem Modell die Elemente Gold (79) und Quecksilber (80) die ersten Elemente einer nach rechts geschriebenen Achtergruppe sind. Im Standardmodell folgen die Elemente Thallium (81) bis Radon (86) auf der 6p – Schale. Auch hier findet man zwischen Thallium und Quecksilber eine energetische Kante in ähnlicher Höhe wie zwischen Gold und Platin, so dass hier nicht entschieden werden kann, welches Modell besser passt.

Es folgen die Elemente Francium (87) und Radium (88) auf dem inneren Elektronenring. Ihren Elektronenachtundzwanzigstel vorausgegangen sind dort die beiden Elementlücken auf den roten Bezirken. Wie bei Lutetium und später auch bei Lawrencium bewirken diese Lücken extrem niedrige erste Ionisierungsenergien (4,1 eV, Francium und 5,3 eV, Radium, siehe Tab.6).

Ausgeprägte energetische Kanten lassen sich ab jetzt mangels tatsächlicher Messwerte nicht mehr ausmachen, auch wenn man die grünen und roten theoretischen Werte mit einbezieht.

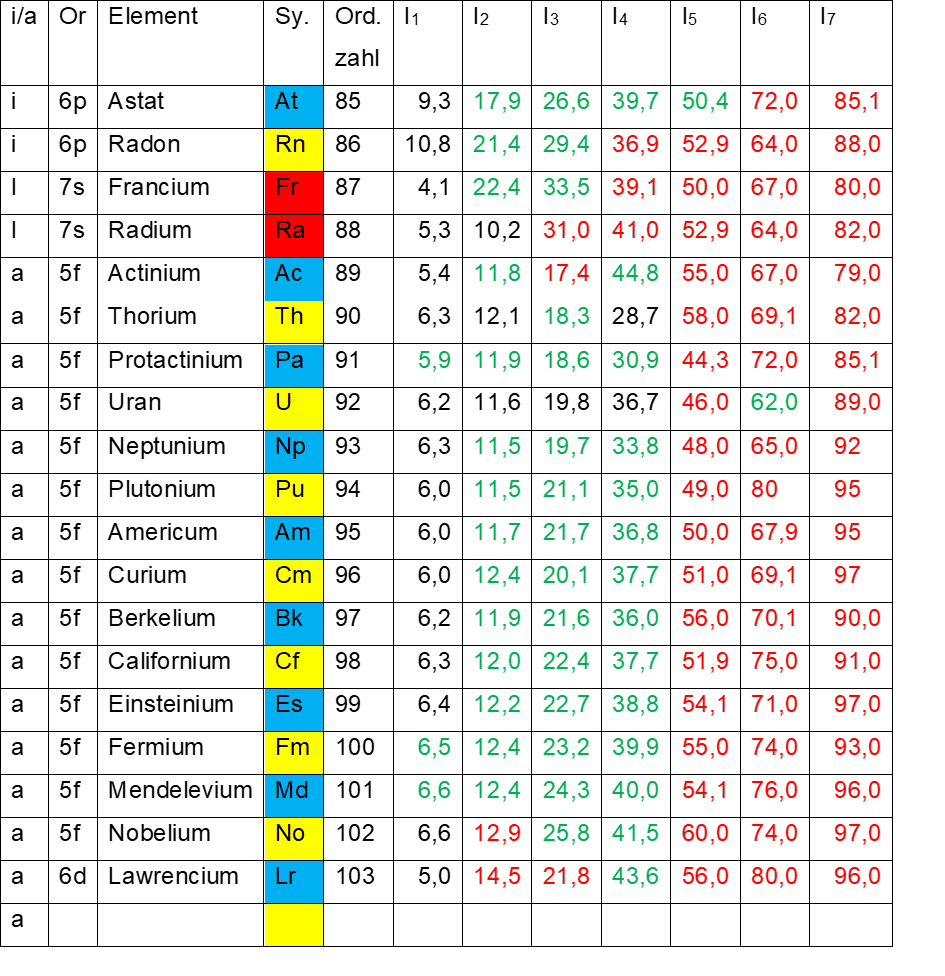
Tab. 6: Ionisierungsenergien I₁ – I₇ der Elemente 85 – 103
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte

Es folgt die Gruppe der Actiniden (Actinium, 89 bis Lawrencium, 103), die nach links geschrieben sind auf dem äußeren Elektronenring. Hier finden sich wieder ganz niedrige erste Ionisierungsenergien (5,0 bis 6,6 eV).

Nach Lawrencium gibt es wieder eine vier Elemente breite Lücke genau wie am Ende der Lanthaniden. Die erste Lücke nach Lawrencium befindet sich auf dem äußeren Elektronenring (gelbe Sektoren). Wie bei Lutetium besitzt Lawrencium die niedrigste erste Ionisierungsenergie seiner Gruppe (5,0 eV), so dass auch hier manche Wissenschaftler zweifeln, ob sich Lawrencium an der richtigen Stelle des Periodensystems befindet.

Tab. 7: Ionisierungsenergien I₁ – I₇ der Elemente 103 – 118
Schwarz Messwerte
Grün inter – oder extrapolierte Werte
Rot theoretische Werte
Lila Werte aus internetchemie.php

Der äußere Elektronenring ist nun voll. Er hat all alle seine Plätze (rote, blaue und gelbe Sektoren) vergeben.

Die zweite und dritte Elementenlücke befindet sich demnach in den roten Sektoren des inneren Elektronenrings. Die vierte Lücke (blaue Bezirke) befindet sich ebenfalls zwangsläufig auf dem inneren Elektronenring. Dort geht es auch weiter mit der nach rechts geschriebenen Siebenergruppe (Rutherfordium, 104 bis Darmstadtium, 110). In dieser Gruppe gibt es keine tatsächlichen Messwerte mehr.

Es folgt die letzte nach rechts geschriebene Achtergruppe Roentgenium (111) bis Oganesson (118). Für diese Achtergruppe gibt es Werte aus internetchemie.php, wobei allerdings unklar bleibt, ob es sich um Messwerte oder theoretisch berechnete Werte handelt (siehe Tab.7).

Folgt man den graphisch aufgetragenen Werten der Elemente 104 bis 118 (siehe Abb.5), so erkennt man den sprunghaften Verlauf für nach rechts geschriebene Gruppen.

Im Standardmodell belegen die Elemente Actinium (89) bis Nobelium (102) die 5f – Schale. Das Letzte Element der Actiniden Lawrencium befindet sich auf der 6d – Schale, wie auch die Elemente Rutherfordium (104) bis Copernicum (112). Die Elemente Nihonium (113) bis Oganesson (118) finden sich dann auf der 7p – Schale. Mit der Schaleneinteilung des Standardmodells wird so verschleiert, dass die Actiniden eigentlich genau wie die Lanthaniden 15 Elemente umfassen (14 f – Elektronen plus 1 d – Elektron). In meinem Modell handelt es sich dagegen um jeweils zwei nach links geschriebene Achtergruppen ( eine Achtergruppe plus eine Siebenergruppe mit einer Elementenlücke).

Im Standardmodell folgen neun d – Elektronenelemente plus sechs p – Elektronenelemente, wohingegen in meinem Modell eine 1 Elementenlücke plus Siebenergruppe und eine letzte Achtergruppe folgen.

Betrachtet man die in den Tabellen 1 – 7 aufgeführten Ionisierungsenergien I₁ – I₇, so zeigt sich in den ersten zwei Dritteln des Periodensystems eine weitgehende Übereinstimmung mit meinem neuen Modell – insbesondere an den „energetischen Kanten“ – im letzten Drittel sind die Unterschiede zwischen meinem und dem Standardmodell nicht mehr so gravierend. Allerdings passen die Lanthaniden und die Actiniden (jeweils 15 Elemente) besser in mein neues Schema als ins Standardmodell. Außerdem bietet mein Modell eine vernünftige Erklärung für die besonders niedrigen ersten Ionisierungsenergien der Elemente Lutetium (71) und Lawrencium (103).

Elektrische Leitfähigkeit und Magnetismus

Bei den Elementen des Periodensystems wird unterschieden zwischen elektrischen Leitern, Halbleitern, elektrischen Nichtleitern und Edelgasen, wobei die Edelgase zu den elektrischen Nichtleitern gehören (siehe Tab. 8 und Tab. 9).

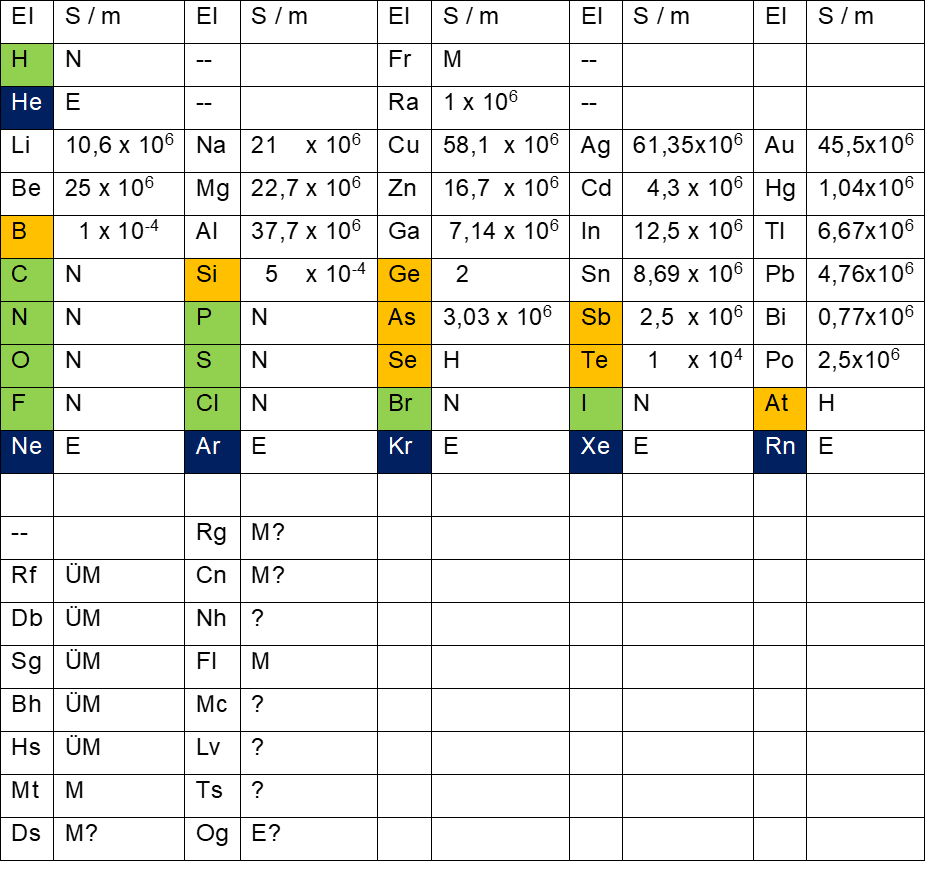
Tab. 8: elektrische Leitfähigkeit der Elemente des inneren Elektronenrings
Grün: elektrische Nichtleiter Orange: Halbleiter Blau: Edelgase
S / m = Siemens pro Meter El = Element

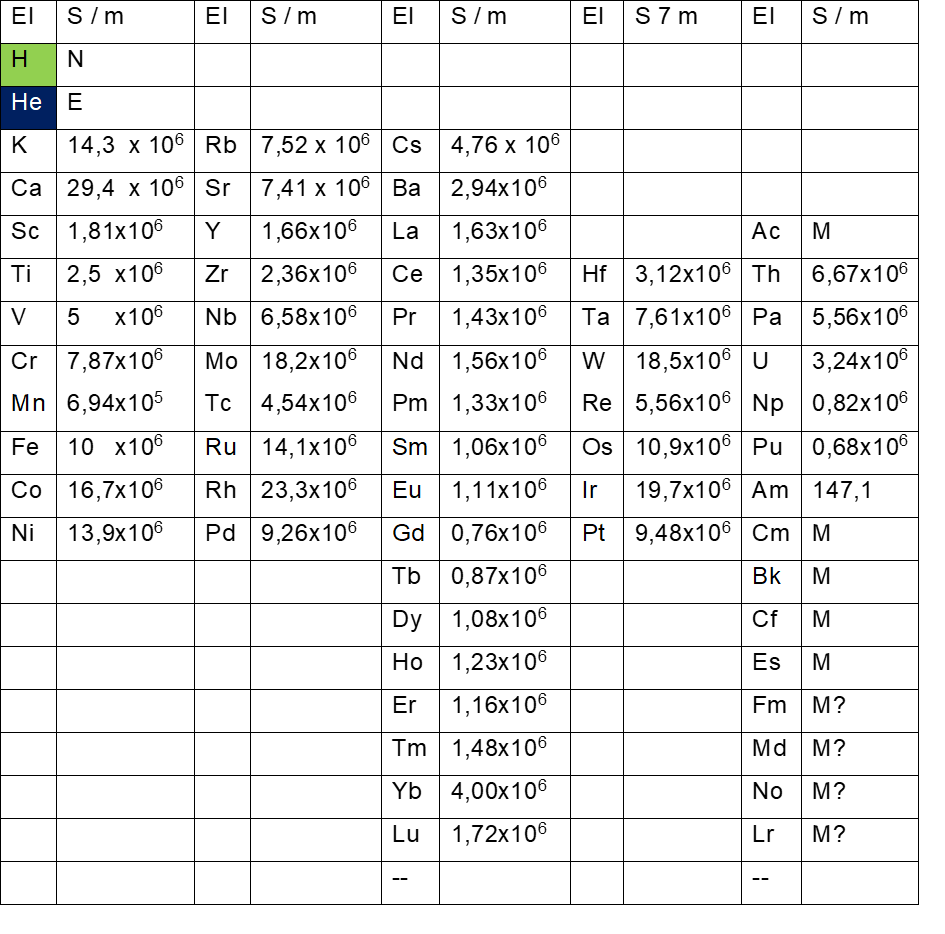
Tab. 9: elektrische Leitfähigkeit der Elemente des äußeren Elektronenrings

Dabei zeigt sich, dass sich auf dem äußeren Elektronenring ausschließlich elektrisch leitfähige Elemente befinden ( Ausnahmen H und He, die ihre Elektronenachtundzwanzigstel auf beide Ringe verteilen ). Ab Element 89 (Actinium) auf dem äußeren Ring finden sich bei Wikipedia nur noch selten Angaben zur elektrischen Leitfähigkeit, die Wissenschaft geht aber davon aus, dass es sich um Metalle handelt.

Auf dem inneren Elektronenring dagegen finden sich die elektrischen Nichtleiter und die Halbleiter sowie alle Edelgase im Periodensystem. Zu Beginn jeder Achtergruppe innen herrscht hohe elektrische Leitfähigkeit, die dann mit zunehmender Elektronenanzahl in Halbleiter und elektrische Nichtleiter übergeht. Zu Beginn (Achtergruppe Lithium – Neon) gibt es zwei Elemente, die elektrische Leiter sind, bevor mit Bor der erste Halbleiter auftritt. In der nächsten beiden Achtergruppen (Natrium – Argon und Kupfer – Krypton) sind es drei elektrische Leiter vor den folgenden Halbleitern. In der Achtergruppe Argentum – Xenon sind es dann vier elektrische Leiter, in der verbleibenden Achtergruppe Gold – Radon sogar sechs elektrische Leiter. Ab Element 104 (Rutherfordium) finden sich keine Angaben zur elektrischen Leitfähigkeit bei Wikipedia. Es handelt sich wahrscheinlich überwiegend um Übergangsmetalle und Metalle. Alle sind radioaktiv und können nur künstlich hergestellt werden bei meist sehr kurzen Halbwertszeiten, was jede Art Messung schwierig werden lässt.

Magnetismus

Wir unterscheiden hauptsächlich den Diamagnetismus, den Paramagnetismus und den Ferromagnetismus.

Diamagnetismus

Bringt man eine Substanz in ein magnetisches Feld, so induziert dieses in den Elektronenhüllen der Atome einen Strom, dessen Magnetfeld nach der Lenzschen Regel dem äußeren entgegengerichtet ist. Diamagnetismus führt so zu einer Abschwächung des Magnetfeldes in der Substanz(Quelle: Wikipedia).

Paramagnetismus

Besitzen die Atome, Ionen oder Moleküle eines Materials ein magnetisches Moment, so richten sich diese parallel zum äußeren Magnetfeld aus. Dies bewirkt eine Verstärkung des Magnetfeldes im Material. Bei einem idealen Paramagneten sind die einzelnen magnetischen Momente voneinander isoliert. Darum bricht das innere Magnetfeld nach Entfernen des äußeren Magnetfelds wegen der Wärmebewegung der Teilchen zusammen. Dementsprechend nimmt der Paramagnetismus mit steigender Temperatur ab (Quelle: Wikipedia).

Ferromagnetismus

Beim Ferromagnetismus sind die magnetischen Momente einzelner Teilchen nicht unabhängig voneinander, sondern richten sich spontan parallel aus. Die Kopplung der magnetischen Momente erstreckt sich aber nicht über das ganze Material, sondern ist auf kleine Bereiche, die Weissschen Bezirke, beschränkt. Typische Längenskalen sind zehn Nanometer bis wenige Mikrometer. Die Ausrichtung der Weissschen Bezirke ist statistisch verteilt, so dass der Gesamtkörper unmagnetisch erscheint. Durch ein äußeres Magnetfeld kann man die Bezirke gleich ausrichten. Diese Gleichrichtung bleibt auch nach Entfernen des äußeren Feldes erhalten, so dass man eine permanente Magnetisierung erhält. Die Magnetisierung kann durch Erhitzen über die ferromagnetische Curie-Temperatur zerstört werden (Quelle: Wikipedia). Die Tab. 10 und Tab. 11 geben einen Überblick über die magnetischen Eigenschaften der Elemente des Periodensystems.

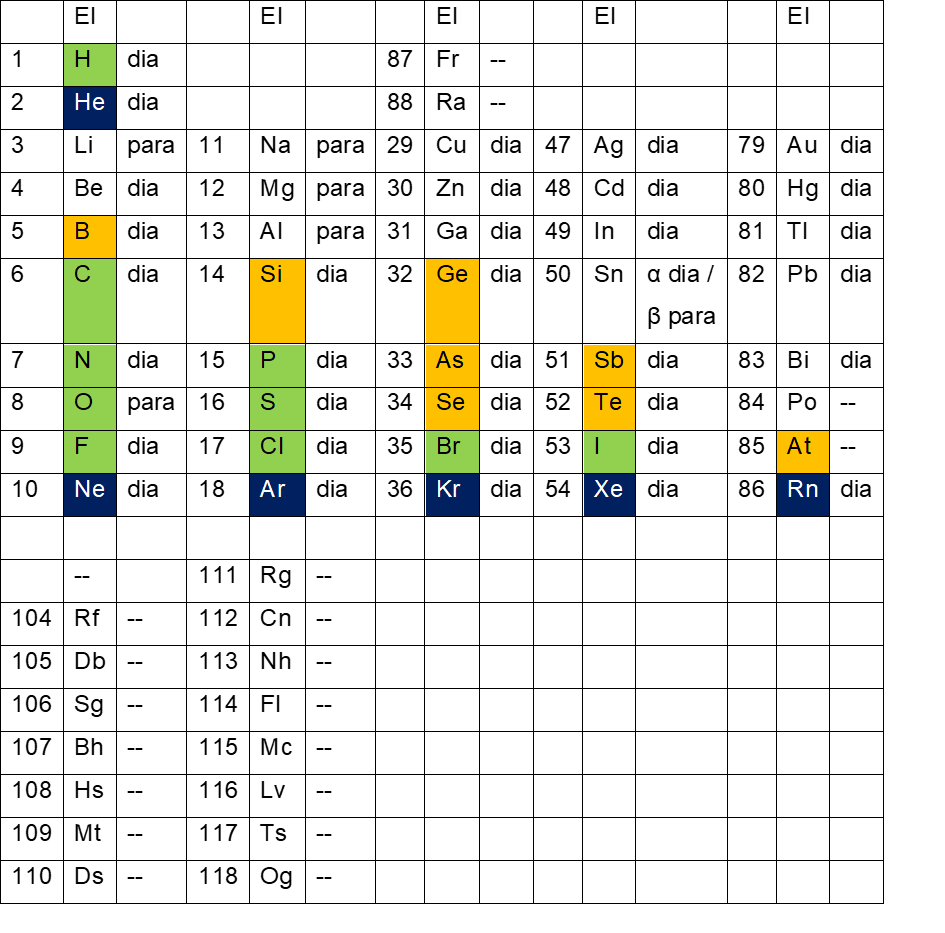
Tab.10: Innerer Elektronenring, magnetische Eigenschaften

Tab.11: Äußerer Elektronenring, magnetische Eigenschaften

Alle Elemente auf dem äußeren Elektronenring sind para – oder ferromagnetisch. Von den Elementen ab 89 Actinium sind die magnetischen Eigenschaften zum großen Teil nicht bekannt. Auf dem inneren Elektronenring sind die Elemente überwiegend diamagnetisch. So lange sich auf dem äußeren Elektronenring noch keine Elemente außer Wasserstoff und Helium befinden, sind die Elemente auf dem inneren Elektronenring ( 3 Lithium bis 18 Argon ) entweder dia – oder paramagnetisch. Sobald aber die Elemente ab 21 Scandium außen dazukommen, sind alle Elemente des inneren Elektronenrings diamagnetisch. Anscheinend besitzt der äußere Elektronenring, falls sich Elemente darauf befinden, eine für Magnetismus abschirmende Wirkung.

Im neuen Modell befinden sich die Elemente der Achtergruppe 21 Scandium bis 28 Nickel auf dem äußeren Elektronenring. Sie sind paramagnetisch. Die Elemente der Achtergruppe 29 Kupfer bis 36 Krypton befinden sich innen und sind alle diamagnetisch.

Im Standardmodell hingegen bekleiden die Elemente 21 Scandium bis 30 Zink die die 3d – Schale, es handelt sich um 10d – Elektronen, wobei die ersten acht (Scandium bis Nickel) paramagnetisch, die letzten beiden (Kupfer und Zink) diamagnetisch sind.

Dasselbe passiert noch einmal bei der Achtergruppe 39 Yttrium bis 46 Palladium. Im neuen Modell befinden sich diese Elemente auf dem äußeren Elektronenring und sind alle paramagnetisch. Die folgende Achtergruppe 47 Argentum bis 54 Xenon befindet sich auf dem inneren Elektronenring und diese Elemente sind alle diamagnetisch (Ausnahme: 50 Sn kann sowohl dia – als auch paramagnetisch sein).

Im Standardmodell finden sich hier die d – Elektronen der 4d – Schale (39 Yttrium bis 48 Cadmium. Hier sind Yttrium bis Palladium wieder paramagnetisch und Argentum und Cadmium diamagnetisch.

Dieses Spiel begegnet uns noch ein drittes mal. Im neuen Modell befinden sich die Elemente der Siebenergruppe 72 Hafnium bis 78 Platin auf dem äußeren Ring und sind damit paramagnetisch. Die Elemente der Achtergruppe 79 Aurum bis 86 Radon haben ihren Platz auf dem inneren Elektronenring und sind alle diamagnetisch.

Im Standardmodell handelt es sich um die d – Elektronen der 5d – Schale (72 Hafnium bis 80 Quecksilber). Hier sind 72 Hafnium bis 78 Platin paramagnetisch und die Elemente 79 Aurum und 80 Quecksilber wieder diamagnetisch.

Im Fall der d – Elektronen der 3d -, 4d – und 5d – Schale ist das neue Modell dem Standardmodell deutlich überlegen, denn es beschreibt den Unterschied zwischen dem Para – und dem Diamagnetismus der beteiligten Elemente durchgängig mit einem Wechsel des Elektronenrings, wohingegen das Standardmodell dafür keine Erklärung bietet.

Im Fall der f – Elektronen im Standardmodell der Lanthaniden (57 Lanthan bis 71 Lutetium) handelt es sich um 14 f – Elektronen (57 Lanthan – 70 Ytterbium) und ein d – Elektron (71 Lutetium). Im neuen Modell befinden sich alle 15 Elemente auf dem äußeren Elektronenring (Achtergruppe 57 Lanthan bis 64 Gadolinium und Achtergruppe 65 Terbium bis 71 Lutetium mit anschließender Elementenlücke).

Auch hier begegnet uns dieser Fall nochmals bei den Actiniden (89 Actinium bis 103 Lawrencium). Im Standardmodell finden sich hier wieder 14 f – Elektronen und als Abschluss ein d – Elektron (103 Lawrencium). Im neuen Modell dagegen befinden sich diese Elemente als zwei Achtergruppen (1 Achtergruppe plus 1 Siebenergruppe mit anschließender Elementenlücke) auf dem äußeren Elektronenring.

Im Vergleich mit dem Standardmodell bildet das neue Modell die Eigenschaften der elektrischen Leitfähigkeit und des Magnetismus der Elemente des Periodensystems viel besser ab.

Das Bindungsmodell von Wasser

Ein bisher ungeklärtes Faktum in der Atomphysik ist die Verbindung von zwei Wasserstoffatomen mit einem Atom Sauerstoff zu einem Wassermolekül. Nach der herrschenden Orbitaltheorie des Standardmodells sollte der Bindungswinkel zwischen den Wasserstoffatomen und dem Sauerstoffatom 109,5° betragen (Tetraederwinkel des sp₃-Hybridorbitals). In Wirklichkeit liegt der Winkel aber bei 104,5°. Im hier vorgestellten Modell binden die Achtundzwanzigstelelektronen von Wasserstoff in ihren roten Bezirken und die des Sauerstoffs (geradzahliges Element, bindende Elektronenachtundzwanzigstel in den gelben Sektoren/Bezirken) in den Bezirken Gelb 1a und Gelb 3b (siehe Abb.7), so dass der in der Natur vorkommende Bindungswinkel von 104,5° ganz exakt realisiert werden kann.

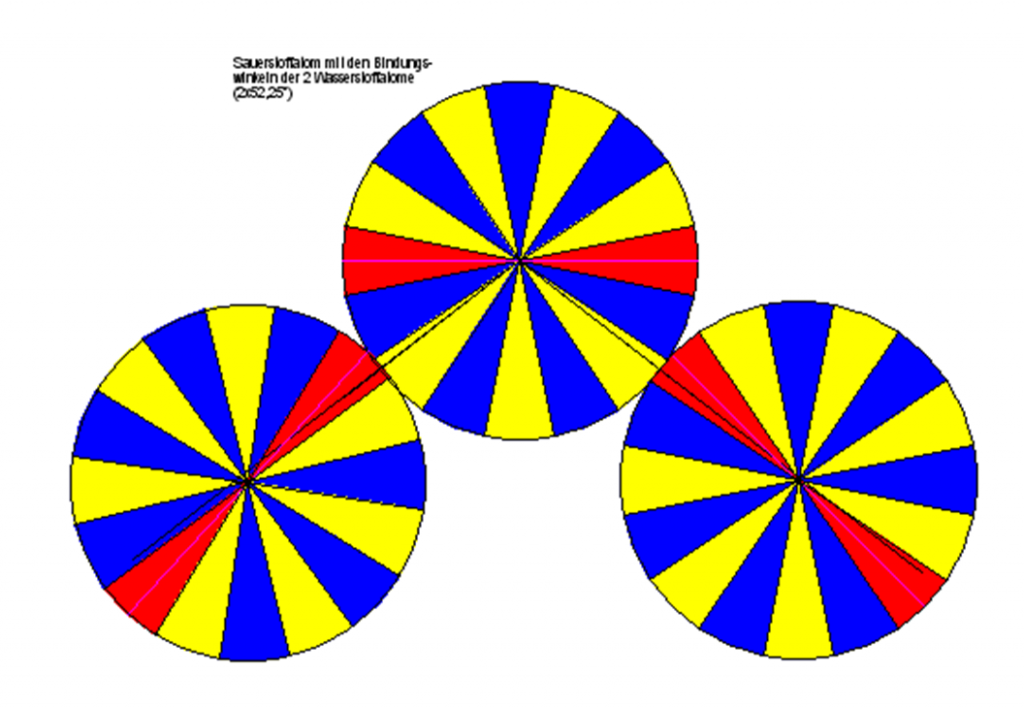
Abb.7: Bindungsmodell von Wasser. Der besseren graphischen Darstellbarkeit wegen ist hier nur der bindende innere Elektronenring als Kreis gezeichnet. Die Abbildung ist nicht maßstabsgerecht, in Wirklichkeit ist das Sauerstoffatom größer als die beiden Wasserstoffatome.

Benzol

Benzol ist ein chirales Molekül, das heißt, obwohl alle C-C-Bindungen gleichwertig sind, sehen die Kohlenstoffatome in der Röntgenstrukturanalyse nicht alle gleich aus und haben auch nicht alle den gleichen Bindungsabstand. Die C-Atome 1 und 4, 2 und 5 und 3 und 6 entsprechen einander, es handelt sich um chirale Symmetrie (siehe Abb.8).

Abb.8: Chiralität des Benzolrings. Dargestellt ist der bindende (innere kleinere) Elektronenring als Kreis. Der Kreismittelpunkt ist der Atomkern, der zweite (äußere größere) hier nicht gezeichnete Elektronenring steht jeweils senkrecht auf dem ersten gezeichneten.

Das hier vorgestellte Elektronenmodell in Verbindung mit der Neueinteilung des Periodensystems der Elemente bietet Erklärungsmöglichkeiten für Unklarheiten (Chiralität des Benzolrings) und auch Widersprüchlichkeiten (Bindungswinkel von Wasser: 109,5° Tetraederwinkel versus 104,5° in der Realität) im geltenden Standardmodell.